1. B-树
二叉树中我们已经介绍过,为了减少磁盘IO次数,我们就需要把原本瘦高的二叉树,变为胖矮的树。这就是B-树的特征。
读B树,不是B减树
B树和平衡二叉树稍有不同的是B树属于多叉树又名平衡多路查找树(查找路径不只两个),数据库索引技术里大量使用者B树和B+树的数据结构
- 定义任意非叶子节点最多有M个儿子,且M>2; (M一般取决于磁盘页的大小)
- 根节点的儿子数为[2,M];
- 除根节点以外的非叶子节点的儿子数为[M/2,M];
- 每个节点存放至少M/2-1(取上整)和至多M-1个关键字
- 非叶子节点的关键字个数=指向儿子节点的指针的个数-1;
- 非叶子节点的关键字:k[i]<k[i+1];
- 非叶子节点的指针:p[1],p[2],·····,p[M];其中p[1]指向的关键字小于k[1]的子树,p[M]指向的关键字大于K[m-1]的子树;
- 所有的叶子节点位于同一层;
下图是来自网络的一张图
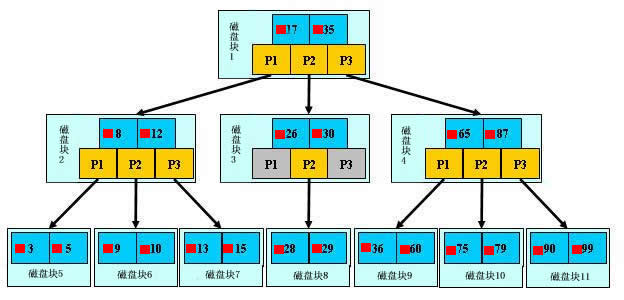
简单理解
- B树将二叉搜索改为了M叉搜索
- 叶子节点非叶子节点都存储数据
- 树的高度比二叉树大大降低
为了提升效率,要尽量减少磁盘 I/O 的次数。实际过程中,磁盘并不是每次严格按需读取,而是每次都会预读。
磁盘读取完需要的数据后,会按顺序再多读一部分数据到内存中,这样做的理论依据是计算机科学中注明的局部性原理:
- 由于磁盘顺序读取的效率很高(不需要寻址时间,只需很少的旋转时间),因此对于具有局部性的程序来说,预读可以提高 I/O 效率。预读的长度一般为页(page)的整倍数。
- MySQL(默认使用 InnoDB 引擎),将记录按照页的方式进行管理,每页大小默认为 16K(可以修改)。
B-Tree 借助计算机磁盘预读机制:每次新建节点的时候,都是申请一个页的空间,所以每查找一个节点只需要一次 I/O;因为实际应用当中,节点深度会很少,所以查找效率很高。
2. B+树
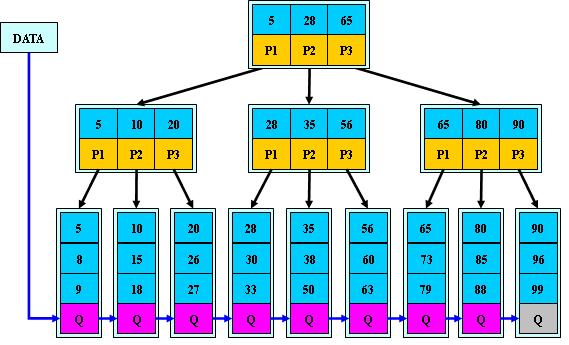
B+树是B树的改进版
- 只有叶子节点存储数据,非叶子节点不存储数据,所有的数据都必须到叶子节点才能获得,每次的查询记录一样
- 叶子节点通过链表从小到大连接
这些改进让B+树比B树更有优势
- 对于范围查询,定位最小值和最大值后,中间的叶子节点就是结果集,而不需要回溯查询
- 只有叶子节点存储数据,数据相对更加紧密,非叶子节点存储记录的KEY,在相同内存下可以比B树存储更多的索引
- 假设一页可以存储1000条记录,那么2层树可以存放
1000*1000条数据,3层树可以存放1000*1000*1000条数据,4层树可以存放1000*1000*1000*1000条数据,所以树的高度一般在2~4层,而通过主键查找只需要2~4次磁盘IO就能在对应的页面找到记录
2.1. 插入
B+树的插入需要考虑3种情况
- 叶子节点和索引节点均未满
- 叶子节点已满,索引节点未满
- 叶子节点,索引节点已满
向下图的B+树(每个节点只能存放3个数据)插入7时,叶子节点和索引节点均未满,直接插入到叶子节点
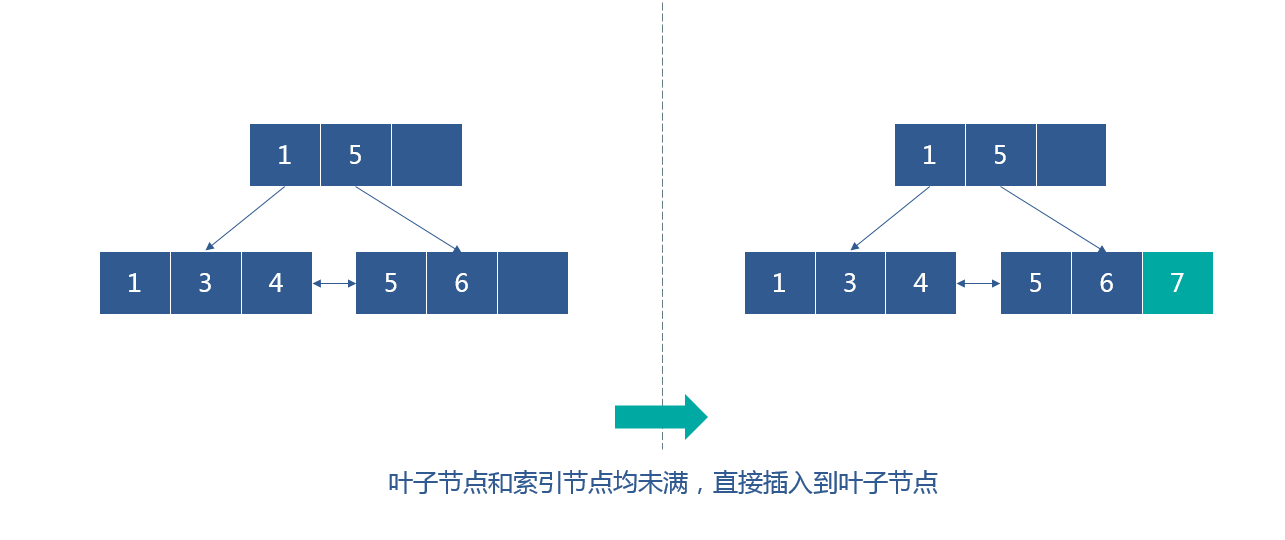
接着插入8,叶子节点已满,需要分裂,选取待分裂节点中间位置的项进行分裂,而索引节点未满,直接将分裂后的索引插入索引节点

继续插入节点20

叶子节点已满,选取待分裂节点中间位置的项进行分裂,分裂后索引节点已满,继续分裂
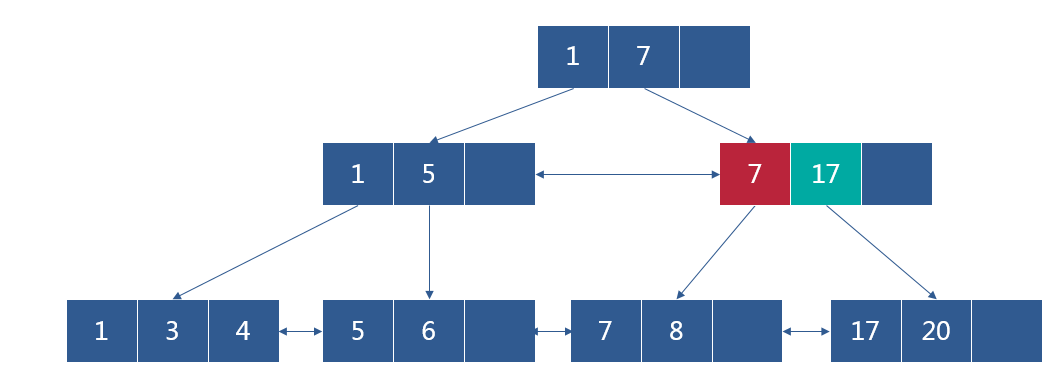
2.2. 删除
B+树的删除也需要考虑多种情况
- 删除后节点的关键字>M/2
- 删除最大最小关键字
- 删除后节点的关键字<M/2,其兄弟结点中含有多余的关键字
- 删除后节点的关键字<M/2,其兄弟结点没有多余的关键字
向下图的B+树(每个节点只能存放3个数据)删除3时,删除后节点的关键字>M/2,不会破坏B+树,可以直接删除
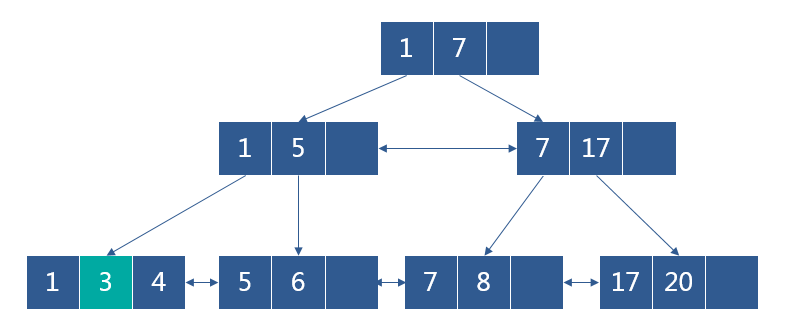
删除后

向下图的B+树删除1时,会导致索引节点的修改
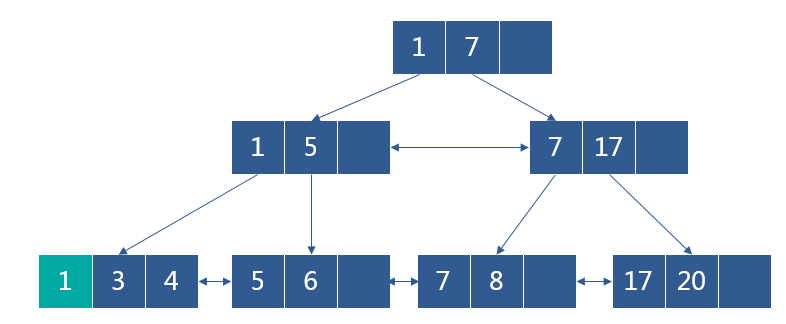
删除后

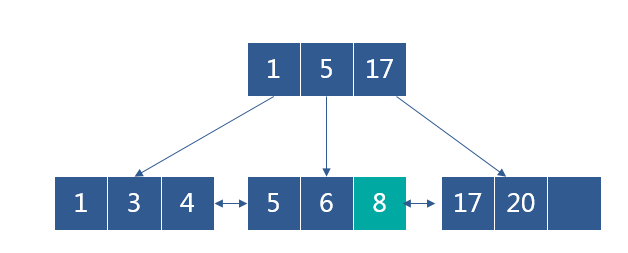
向下图的B+树删除5时,删除后节点的关键字<M/2,如果其兄弟结点中含有多余的关键字,从兄弟结点中借关键字完成删除操作

删除后

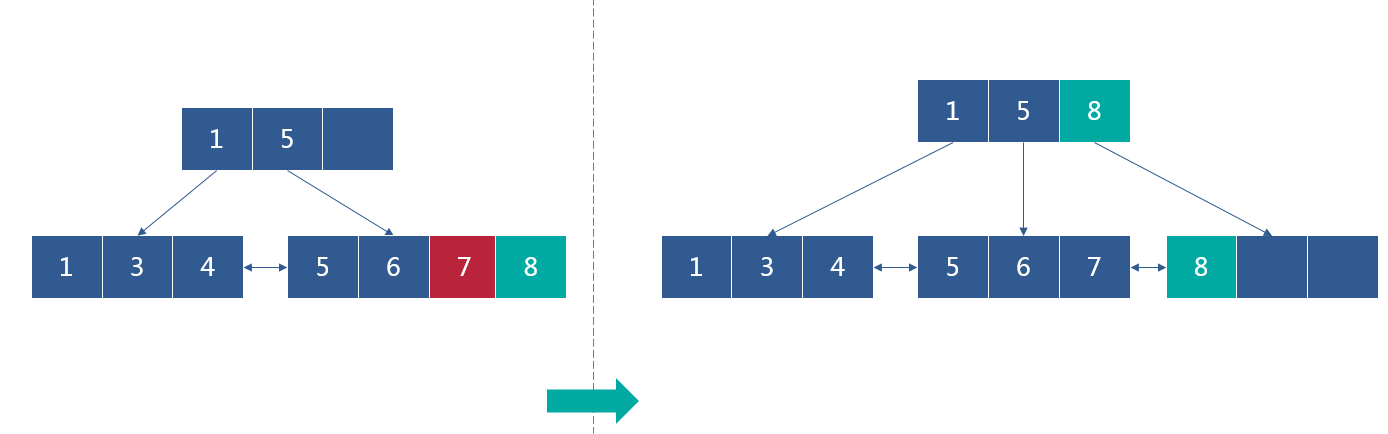
向下图的B+树删除7时,删除后节点的关键字<M/2,如果其兄弟结点中含有多余的关键字,从兄弟结点中借关键字完成删除操作
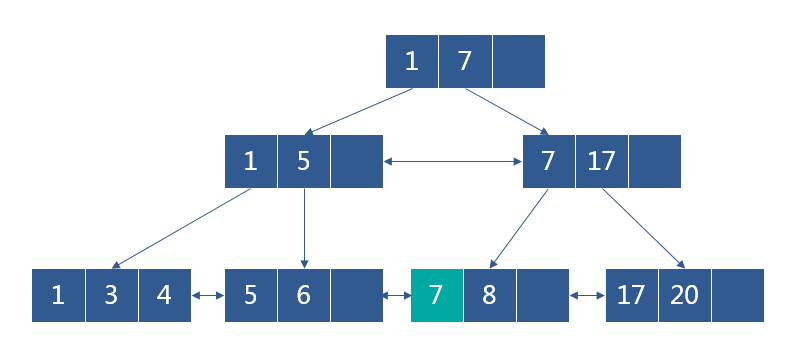
删除后
2.3. 按50%分裂的不足
- 空间利用率不高:按照传统50%的页面分裂策略,索引页面的空间利用率在50%左右;
- 分裂频率较大:针对如上所示的递增插入(递减插入),每新插入4条记录,就会导致最右的叶子页面再次发生分裂;
基于上面的考虑,InnoDb对分裂做了优化,为每个索引页面维护了一个上次插入的位置,以及上次的插入是递增/递减的标识。根据这些信息,InnoDB能够判断出新插入到页面中的记录,是否仍旧满足递增/递减的约束,若满足约束,则采用优化后的分裂策略
- 不移动原有页面的任何记录,只是将新插入的记录写到新页面之中,分裂的代价小
- 原有页面的利用率,仍旧是100%;
但是这个优化仅对递增有效:如果新的插入,不再满足递增插入的条件,而是插入到原有页面,那么就会导致原有页面再次分裂,增加了分裂的概率
所以数据库规范建议使用一列顺序递增的 ID 来作为主键,但不必是数据库的autoincrement字段,只要满足顺序增加即可 。
3. 为什么 MySQL 索引选择了 B+树而不是 B 树?
原因有如下两点:
- B+树更适合外部存储(一般指磁盘存储),由于内节点(非叶子节点)不存储 data,所以一个节点可以存储更多的内节点,每个节点能索引的范围更大更精确。也就是说使用 B+树单次磁盘 I/O 的信息量相比较 B 树更大,I/O 效率更高。
- MySQL 是关系型数据库,经常会按照区间来访问某个索引列,B+树的叶子节点间按顺序建立了链指针,加强了区间访问性,所以 B+树对索引列上的区间范围查询很友好。而 B 树每个节点的 key 和 data 在一起,无法进行区间查找。
4. 参考资料
https://mp.weixin.qq.com/s/YMbRJwyjutGMD1KpI_fS0A
