一个面试题：InnoDB 一棵 B+ 树可以存放多少行数据

InnoDB 存储引擎也有自己的最小储存单元——页（Page），一个页的大小是 16K。假设一行数据的大小是 1K，那么一个页可以存放 16 行这样的数据。在 B+ 树中叶子节点存放数据，非叶子节点存放键值+指针。 可以通过innodb_page_size调整

要回答这个问题，我们需要详细看看B+树的结构

1. B+树结构

ROOT

每一个索引树都是从一个ROOT页开始，它的位置是固定的，永远被保存在InnoDB的数据字典中，ROOT页就是访问索引树的起点。索引树可能只有一个ROOT页，也可能有成百上千个页，这时候就是多级树，并且树的高度超过1。

leaf

索引树的每个页都与叶子（leaf）页或者非叶子（non-leaf）页相关联。叶子页包含实际的行数据，非叶子页只包含指向非叶子页或者叶子页的指针。索引树是平衡的，B+Tree中的B是Balance的意思，而不是Binary。所以，索引树的所有分支有相同的深度。

level

InnoDB索引树中每个页都有一个level值，其中：叶子页level=0，从叶子页往ROOT页，level值递增。ROOT页的level值加1就是树的深度（例如叶子页level=0；ROOT页level=1，那么索引树高度为2）。那些既不是叶子页，也不是ROOT页的页被称为内部（internal）页。

page directory

即页目录（就跟树目录的原理差不多），它是一个大小为2个字节的指向4~8个记录的指针，它的作用是为了改进遍历一个索引页的性能。如果没有页目录，即使二分法查询，如果是拥有大概1000个记录的非叶子页，最多需要近10次的比较（2^10≈1000），并且索引页有多少级，这样的比较要成倍增加。

有了页目录后，我们就可以先用二分法从页目录中找到目标KEY所在的目录，然后通过页目录这个指针，找到目标KEY所在的只有4~8个记录的数组中。我们假设每个页目录平均指向5个记录，那么，1000个记录的非叶子页，需要200个页目录，二分法查找只需要8次（2^8=256），整个遍历过程少了20%的开销。

2. 叶子&非叶子页

对于叶子页和非叶子页，每个记录都包含一个指向下一个记录的指针。它存储了下一个记录的offset值（相对当前页的offset）。一个索引页以下确界（Infimum）开始，以KEY递增的方式连接所有记录，并以上确界（Supremum）结束。

• 叶子页

叶子页包含了其他非KEY的值，这些值也是每个记录中的部分数据（假设表有3列：id, name, age。那么id就是KEY，name和age都是非KEY。KEY和非KEY组成完整的记录）：

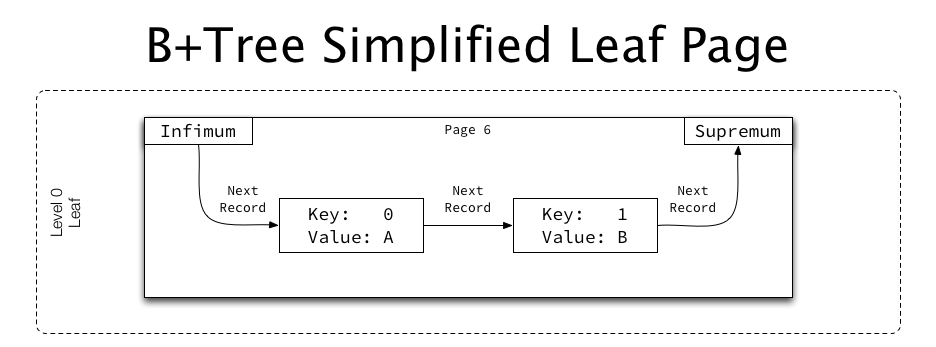
如上图所示，这个叶子页有两个Record：一个Record的Key是0，并且还有非Key的值A；另一个Record的Key是1，并且还有非Key的值B。

• 非叶子页

非叶子页的结构与叶子页的结构大同小异，不同的地方是，非叶子页中保存是子页的页号。而且并不保存一个明确的KEY，而是保存一个Min Key，这个字段表示的是他们指向的子页的最小KEY：

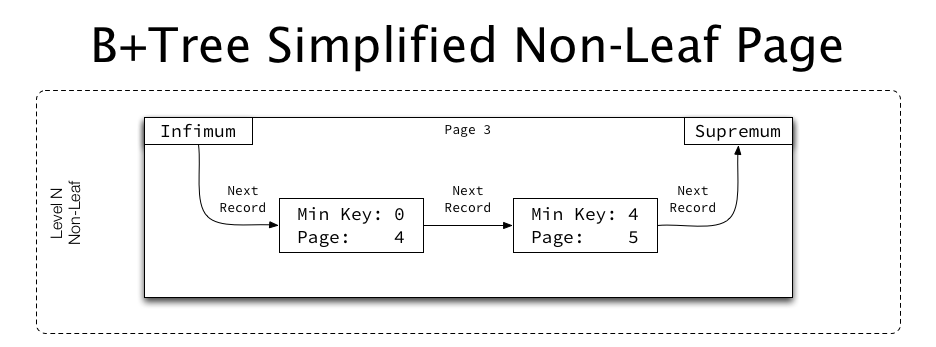
如上图所示，这个非叶子页有两个Record：其中一个Record的Min Key为0，并且Page为4，表示它指向的子页的页号为4，并且它的最小记录为0；我们根据这个视图可以得出结论，这个索引树对应的表的id最小值肯定是0（因为这个页的页号是3，page3表示ROOT页）。

• 相同等级的索引页

许多索引远不止一个页，那么就会有很多级（level）。所以，许多页会被以升序和降序的方式用双向链表串联起来，每个页都包含了指向前一页和下一页的指针。需要注意的是，只有level相同的页才会被串联起来，例如叶子页相互串联成双向链表，level 1 的页相互串联成双向链表。如下图所示，是level=0即叶子页相互串联成的双向链表：

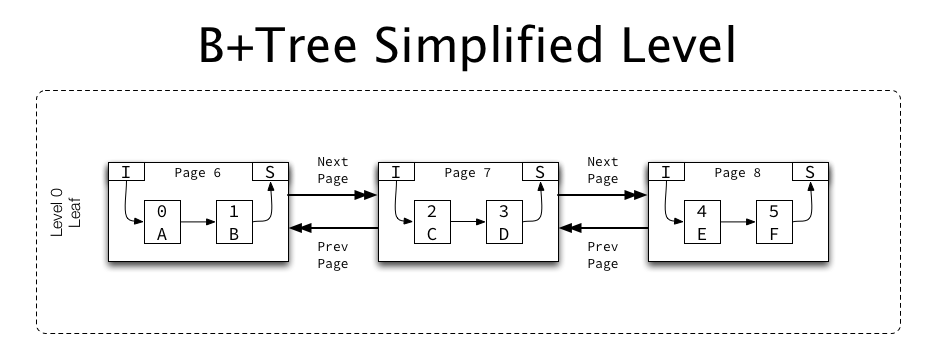
3. 剖析一个索引页

接下来让我们深入研究一个B+Tree索引页的内部，完全掌握一个默认16k大小的索引页里面都保存了一些什么数据，索引页的细节图如下所示：

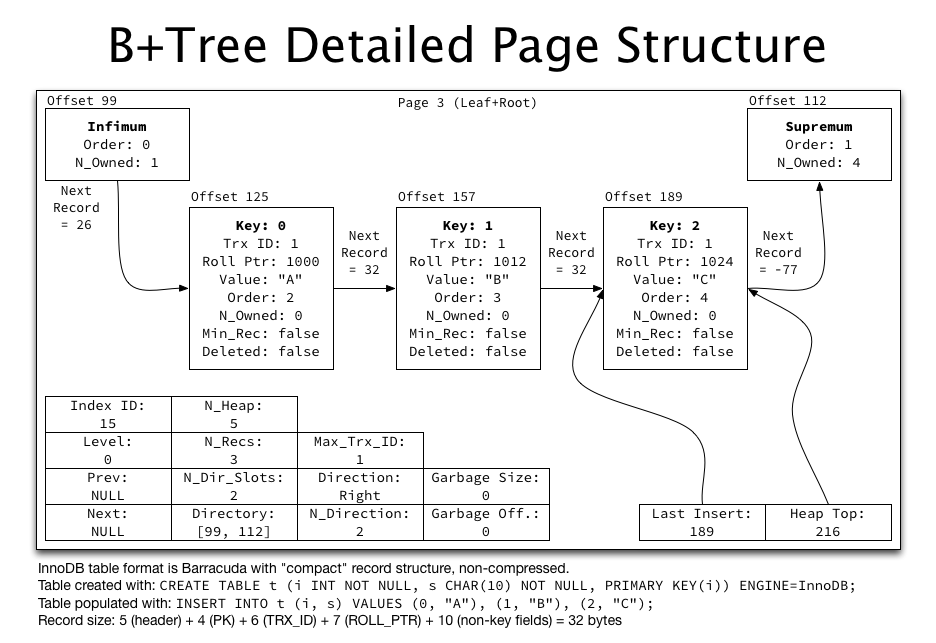
每个索引页都保存了这些些东西：

• 38个字节的FIL Header
• 36个字节的Index Header
• 20个字节的File Segment Header
• 13个字节的Infimum
• 13个字节的Supremum
• 8个字节的FIL Trailer

总计128个字节。

剩下的空间全部用来保存Record Header，Record Data和Page Directory。所以一个16k大小的索引页内容为：128（固定数据占用字节数）+ 39（数据） + 4（Page Directory） + 16213（Free空间，即还没填满） = 16384（每个索引页的大小）

4. InnoDB一棵B+树可以存放多少行数据？

这个问题的简单回答是：约2千万

我们先假设 B+ 树高为 2，即存在一个根节点和若干个叶子节点，那么这棵 B+ 树的存放总记录数为：根节点指针数*单个叶子节点记录行数。

假设一行的数据大小为1K，单个叶子节点（页）中的记录数=16K/1K=16

那么现在我们需要计算出非叶子节点能存放多少指针？

我们假设主键 ID 为 bigint 类型，长度为 8 字节，而指针大小在 InnoDB 源码中设置为 6 字节，这样一共 14 字节。那么非叶子节点的记录数=16384字节/14=1170

16*1024 = 16384

那么可以算出一棵高度为 2 的 B+ 树，能存放 1170*16=18720 条这样的数据记录。

一棵高度为 3 的 B+ 树，能存放 1170*1170*16=21902400 条这样的数据记录。

所以在 InnoDB 中 B+ 树高度一般为 1-3 层，它就能满足千万级的数据存储。 在查找数据时一次页的查找代表一次 IO，所以通过主键索引查询通常只需要 1-3 次 IO 操作即可查找到数据。

5. 怎么得到 InnoDB 主键索引 B+ 树的高度？

在 InnoDB 的表空间文件中，约定 page number 为 3 的代表主键索引的根页，而在根页偏移量为 64 的地方存放了该 B+ 树的 page level。

如果 page level 为 1，树高为 2，page level 为 2，则树高为 3。即 B+ 树的高度=page level+1；下面我们将从实际环境中尝试找到这个 page level。

SELECT
b.name, a.name, index_id, type, a.space, a.PAGE_NO
FROM
information_schema.INNODB_SYS_INDEXES a,
information_schema.INNODB_SYS_TABLES b
WHERE
a.table_id = b.table_id AND a.space <> 0;

下面完全摘自参考资料

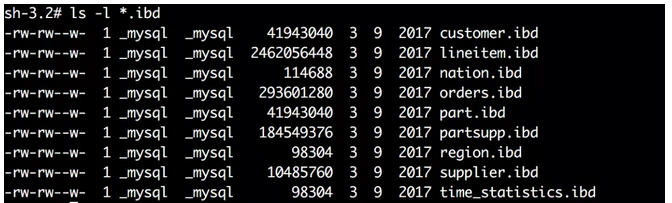
可以看出数据库 dbt3 下的 customer 表、lineitem 表主键索引根页的 page number 均为 3，而其他的二级索引 page number 为 4。

下面我们对数据库表空间文件做想相关的解析：

因为主键索引 B+ 树的根页在整个表空间文件中的第 3 个页开始，所以可以算出它在文件中的偏移量：16384*3=49152（16384 为页大小）。

另外根据《InnoDB 存储引擎》中描述在根页的 64 偏移量位置前 2 个字节，保存了 page level 的值。

因此我们想要的 page level 的值在整个文件中的偏移量为：16384*3+64=49152+64=49216，前 2 个字节中。

接下来我们用 hexdump 工具，查看表空间文件指定偏移量上的数据：

• linetem 表的 page level 为 2，B+ 树高度为page level+1=3。
• region 表的 page level 为 0，B+ 树高度为 page level+1=1。
• customer 表的 page level 为 2，B+ 树高度为 page level+1=3。

这三张表的数据量如下：

lineitem 表的数据行数为 600 多万，B+ 树高度为 3，customer 表数据行数只有 15 万，B+ 树高度也为 3。

可以看出尽管数据量差异较大，这两个表树的高度都是 3。换句话说这两个表通过索引查询效率并没有太大差异，因为都只需要做 3 次 IO。

那么如果有一张表行数是一千万，那么他的 B+ 树高度依旧是 3，查询效率仍然不会相差太大。region 表只有 5 行数据，当然他的 B+ 树高度为 1。

6. 为什么MySQL的索引要使用B+树而不是其它树形结构？比如B树？

他的简单版本回答是：

因为B树不管叶子节点还是非叶子节点，都会保存数据，这样导致在非叶子节点中能保存的指针数量变少（有些资料也称为扇出），指针少的情况下要保存大量数据，只能增加树的高度，导致IO操作变多，查询性能变低；

7. 参考资料

https://mp.weixin.qq.com/s/BWlkrHiB-uP6fDnsxtKU0Q

https://mp.weixin.qq.com/s/CgMUV_rEQYtIRfwW12OBmA

https://blog.jcole.us/2013/01/02/on-learning-innodb-a-journey-to-the-core/