快速排序又称划分交换排序（partition-exchange sort），简称快排，一种排序算法，最早由东尼·霍尔提出。在平均状况下，排序n个项目要O(nlogn)次比较。在最坏状况下则需要O(n^2)次比较，但这种状况并不常见。事实上，快速排序O(nlogn)通常明显比其他算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地达成。

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。快速排序又是一种分而治之思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。

快速排序的最坏运行情况是 O(n²)，比如说顺序数列的快排。但它的平摊期望时间是 O(nlogn)，且 O(nlogn) 记号中隐含的常数因子很小，比复杂度稳定等于 O(nlogn) 的归并排序要小很多。所以，对绝大多数顺序性较弱的随机数列而言，快速排序总是优于归并排序。

算法步骤

从数列中挑出一个元素，称为 “基准”（pivot）;
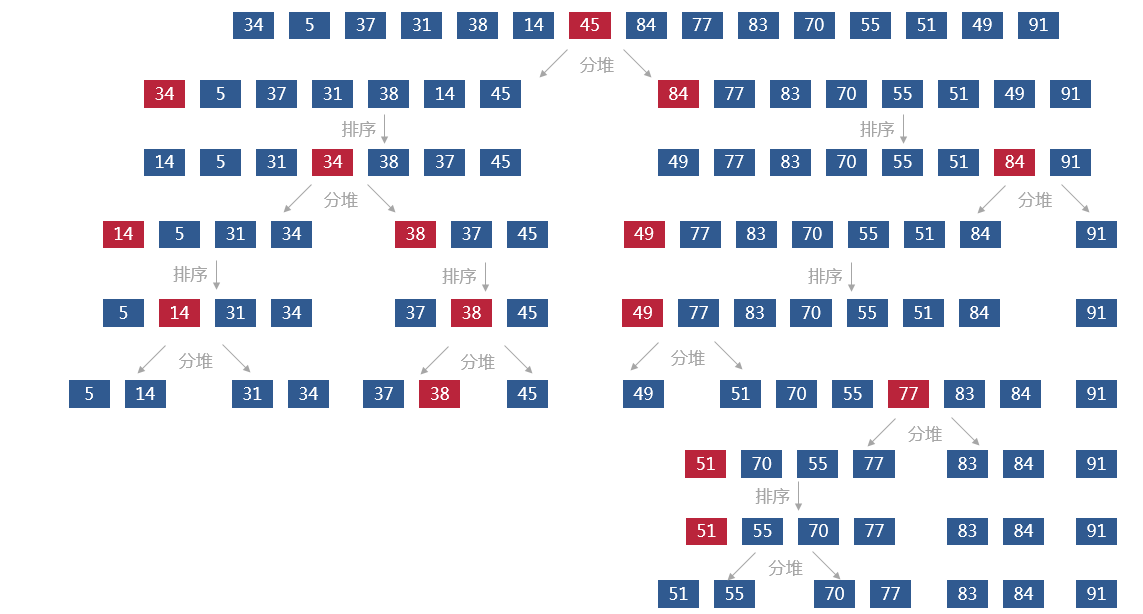
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序；

标准实现Lomuto分区

第一趟排序

分治

源码

  public void sort(int[] array) {
    quickSort(array, 0, array.length - 1);
  }
  
  private void quickSort(int[] arr, int left, int right) {
    if (left < right) {
      int partitionIndex = partition(arr, left, right);
      quickSort(arr, left, partitionIndex - 1);
      quickSort(arr, partitionIndex + 1, right);
    }
  }
  
  private int partition(int[] arr, int left, int right) {
    // 设定基准值（pivot）
    int pivot = left;
    int index = pivot + 1;
    for (int i = index; i <= right; i++) {
      if (arr[i] < arr[pivot]) {
        swap(arr, i, index);
        index++;
      }
    }
    swap(arr, pivot, index - 1);
    return index - 1;
  }

  private void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
  }

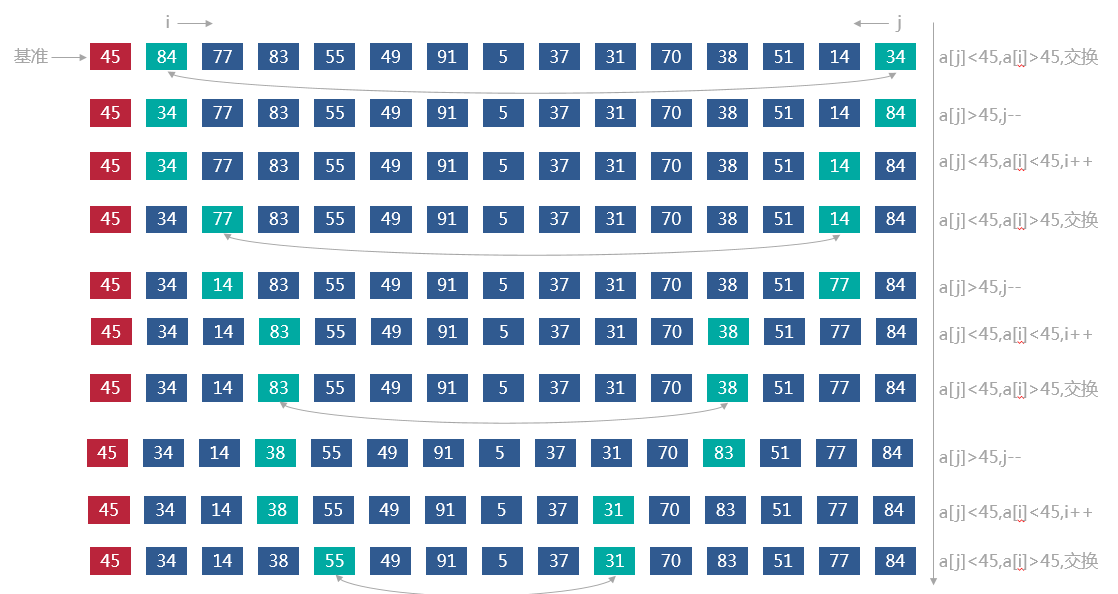
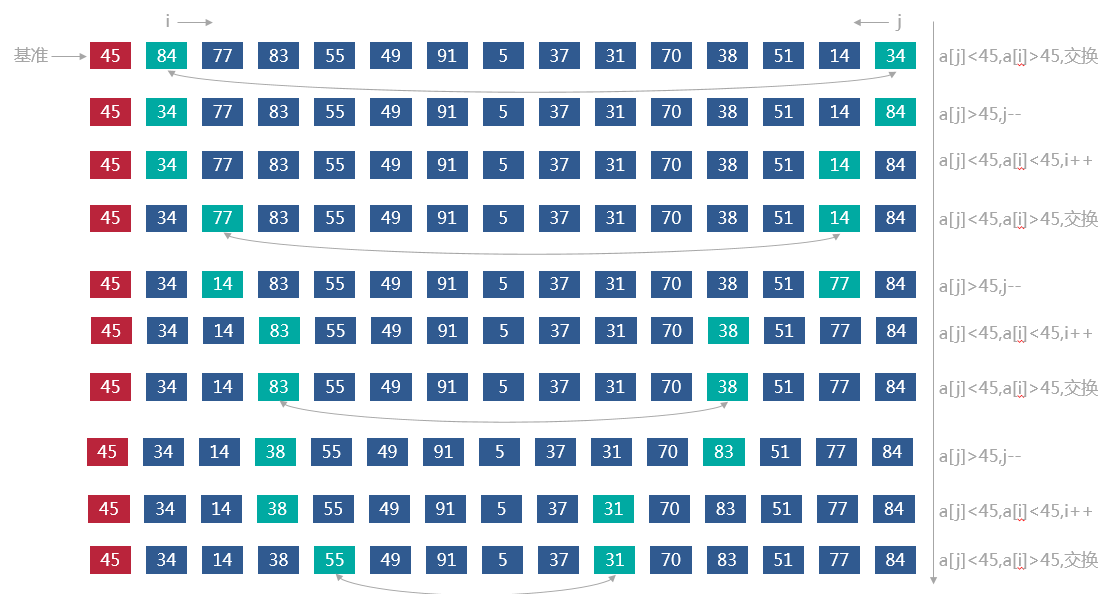
Hoare分区

  private void quickSort(int[] array, int left, int right) {
    if (left < right) {
      int partitionIndex = partition(array, left, right);
      quickSort(array, left, partitionIndex - 1);
      quickSort(array, partitionIndex + 1, right);
    }
  }

  private <T extends Comparable<? super T>> int partition(List<T> list, int left, int right) {
    // 设定基准值（pivot）
    int pivot = left;
    int i = left;
    int j = right;
    while (true) { /* 从表的两端交替向中间扫描 */
      while (j > i && list.get(j).compareTo(list.get(pivot)) > 0) {
        j--;
      }
      while (i < j && list.get(i).compareTo(list.get(pivot)) <= 0) {
        i++;
      }
      if (i >= j) {
        break;
      }
      swap(list, i, j); /* 将比基准记录大的记录交换到高端 */
    }
    swap(list, pivot, j); /* 交换基准值 */
    return j;
  }

基准的选择

基准普遍的有三种选择方法：

固定基准元，一般选取中间值或头部值或尾部值。如果输入序列是随机的，处理时间是可以接受的。如果数组已经有序时或部分有序，此时的分割就是一个非常不好的分割。因为每次划分只能使待排序序列减一，数组全部有序时，此时为最坏情况，快速排序沦为冒泡排序，时间复杂度为O(n^2)。所以此种方式要慎用。
随机基准元，这是一种相对安全的策略。由于基准元的位置是随机的，那么产生的分割也不会总是会出现劣质的分割。在整个数组数字全相等时，仍然是最坏情况，时间复杂度是O(n^2）。实际上，随机化快速排序得到理论最坏情况的可能性仅为1/(2^n）。所以随机化快速排序可以对于绝大多数输入数据达到O(nlogn）的期望时间复杂度。
三数取中，一般是分别取出数组的头部元素，尾部元素和中部元素，在这三个数中取出中位数，作为基准元素。最佳的划分是将待排序的序列分成等长的子序列，最佳的状态我们可以使用序列的中间的值，也就是第N/2个数。可是，这很难算出来，并且会明显减慢快速排序的速度。这样的中值的估计可以通过随机选取三个元素并用它们的中值作为枢纽元而得到。事实上，随机性并没有多大的帮助，因此一般的做法是使用左端、右端和中心位置上的三个元素的中值作为枢纽元。显然使用三数中值分割法消除了预排序输入的不好情形。（简单来说，就是随机取三个数，取中位数）。

三数取中的代码

  private int partition(int[] array, int left, int right) {
    int mid = left + (right - left) / 2;
    if (array[left] > array[right]) {
      SortUtils.swap(array, left, right);	/* 交换左端和右端数据，保证左端较小 */
    }
    if (array[mid] > array[right]) {
      SortUtils.swap(array, mid, right); /* 交换中间和右端数据，保证中间较小 */
    }
    if (array[left] > array[mid]) {
      SortUtils.swap(array, left, mid);	/* 交换左端和中间的数据，保证左端较小 */
    }
    int pivot = left;
    int i = left;
    int j = right;
    while (true) { /* 从表的两端交替向中间扫描 */
      while (j > i && array[j] > array[pivot]) {
        j--;
      }
      while (i < j && array[i] <= array[pivot]) {
        i++;
      }
      if (i >= j) {
        break;
      }
      SortUtils.swap(array, i, j); /* 将比基准记录大的记录交换到高端 */
    }
    SortUtils.swap(array, pivot, j); /* 交换基准值 */
    return j;
  }

优化

优化不必要的交换

普通的快速排序还有一个缺点，那就是会交换一些相同的元素，尤其是当我们处理有大量重复元素的数组时，快排会做很多的无用功，所以由此人们研究出了三切分快排（三路划分），在左右游标的基础上，再增加了一个游标，用于处理和基准元素相同的元素，也就是将数组分为三部分：小于当前切分元素的部分，等于当前切分元素的部分，大于当前切分元素的部分。

优化不必要的替换

  private int partition(int[] array, int left, int right) {
    int pivotValue = array[left];
    int i = left;
    int j = right;
    while (i < j) {
      while (j > i && array[j] >= pivotValue) {
        j--;
      }//出了循环说明要进行移动
      // 采用替换而不是交换的方式进行操作
      array[i] = array[j];

      while (i < j && array[i] <= pivotValue) {
        i++;
      }
      array[j] = array[i];
    }
    array[i] = pivotValue;
    return i;
  }

优化递归操作

大家知道，递归对性能是有一定影响的，quickSort函数在其尾部有两次递归操作。如果待排序的序列划分极端不平衡，递归深度将趋近于n，而不是平衡的log2n，这样就不仅仅是速度快慢的问题了。栈的大小是很有限的，每次递归调用都会耗费一定的栈空间，函数的参数越多，每次递归耗费的空间也越多。因此如果能减少递归，将会大大提高性能。

于是我们对quickSort函数实施尾递归优化

  private void quickSort(int[] arr, int left, int right) {
    while (left < right) {
      int partitionIndex = partition(arr, left, right);
      quickSort(arr, left, partitionIndex - 1);
      // 尾递归
      left = partitionIndex + 1;
    }

  }

当我们将if改为while后，因为第一次递归以后，变量left就没有任何用处了，所以可以将partitionIndex+1赋值给low，再循环后，partition(L,left,right)，其效果等同于quickSort(L,partitionIndex+1,right);。结果相同，但因采用迭代而不是递归的方法可以缩减堆栈深度，从而提高整体性能。

优化小数组时的排序方案

快速排序对于处理小数组（N <= 20）的数组时，快速排序比插入排序要慢，所以在排序小数组时应该切换到插入排序，我们面对小数组的通常的解决办法是对于小的数组不递归的使用快速排序，而代之以诸如插入排序这样的对小数组有效的排序算法。

  private void quickSort(int[] arr, int left, int right) {
    if (right - left < MAX_LENGTH_INSERT_SORT) {
      new InsertSortAlgorithm().sort(arr);
    } else {
      while (left < right) {
        int partitionIndex = partition(arr, left, right);
        quickSort(arr, left, partitionIndex - 1);
        // 尾递归
        left = partitionIndex + 1;
      }
    }
  }

参考资料

https://www.kancloud.cn/maliming/leetcode/740422

https://www.baeldung.com/algorithm-quicksort

https://blog.csdn.net/FTD_SL/article/details/85098476

快速排序

最后更新：2019-12-17