红黑树,本质上来说就是一棵二叉查找树,但它在二叉查找树的基础上增加了着色和相关的规则使得红黑树相对平衡,从而保证了红黑树的查找、插入、删除的时间复杂度最坏为O(log n)。
- 每个节点要么是红的,要么是黑的。
- 根节点是黑的。
- 每个叶节点(叶节点即指树尾端NIL指针或NULL节点)是黑的。
- 如果一个节点是红的,那么它的俩个儿子都是黑的。
- 对于任一节点而言,其到叶节点树尾端NIL指针的每一条路径都包含相同数目的黑节点。
正是红黑树的这5条规则,使得一棵n个节点是红黑树始终保持了logn的高度,从而也就解释了上面我们所说的“红黑树的查找、插入、删除的时间复杂度最坏为O(log n)
“叶子节点” 或”NULL节点”,它不包含数据而只充当树在此结束的指示
从上面的规则我们可以推导出几个隐含规则:
规则:从根节点到叶子节点的最长路径不大于最短路径的 2 倍
根据规则 5中,我们知道从根节点到每个叶子节点的黑色节点数量是一样的,那么纯由黑色节点组成的路径就是最短路径。
根据规则 4 和规则 3,若有红色节点,则必然有一个连接的黑色节点,当红色节点和黑色节点数量相同时,就是最长路径,也就是黑色节点(或红色节点)*2。
规则:新加入到红黑树中的节点为红色节点
因为插入一个红色节点比插入一个黑色节点违背红-黑规则的可能性更小,原因是插入黑色节点总会改变黑色高度(违背规则4),但是插入红色节点只有一半的机会会违背规则3(因为父节点是黑色的没事,父节点是红色的就违背规则3)。另外违背规则3比违背规则4要更容易修正。当插入一个新的节点时,可能会破坏这种平衡性,
黑深度 ——从某个结点x出发(不包括结点x本身)到叶结点(包括叶子结点)的路径上的黑结点个数,称为该结点x的黑深度,记为bd(x),根结点的黑深度就是该红黑树的黑深度。叶子结点的黑深度为0。比如:上图bd(13)=2,bd(8)=2,bd(1)=1
因为每一个红黑树也是一个特化的二叉查找树,因此红黑树上的查找操作与普通二叉查找树上的查找操作相同。然而,在红黑树上进行插入操作和删除操作会导致不 再符合红黑树的规则。恢复红黑树的属性需要少量(O(log n))的颜色变更(实际是非常快速的)和不超过三次树旋转(对于插入操作是两次)。 虽然插入和删除很复杂,但操作时间仍可以保持为 O(log n) 次 。
红黑树能够以O(log2(N))的时间复杂度进行搜索、插入、删除操作。此外,任何不平衡都会在3次旋转之内解决。这一点是AVL所不具备的。
红-黑树通过变色和选中(左旋、右旋)对树进行修正
插入
插入需要考虑几种不同的情况
- 插入根节点:直接变黑
- 父为黑:直接插入
- 父为红,叔叔为红:依次变色
- 父为红,叔叔为黑:
- 左左插入:以祖父节点右旋,搭配变色
- 左右插入:先父节点左旋,然后祖父节点右旋,搭配变色
- 右左插入:先父节点右旋,然后祖父节点左旋,搭配变色
- 右右插入:以祖父节点左旋,搭配变色
这里的旋转在二叉树中做了介绍,不再重复,
下面来一次介绍这几种情况
父为黑
插入66,父节点64的颜色是黑色节点,没有破坏结构,不需要做任何改变

由于黑节点个数至少为红节点的两倍,因此父为黑的情况较多,而这种情况在插入后无需任何调整,这就是红黑树比AVL树插入效率高的原因!
父为红、叔叔为红
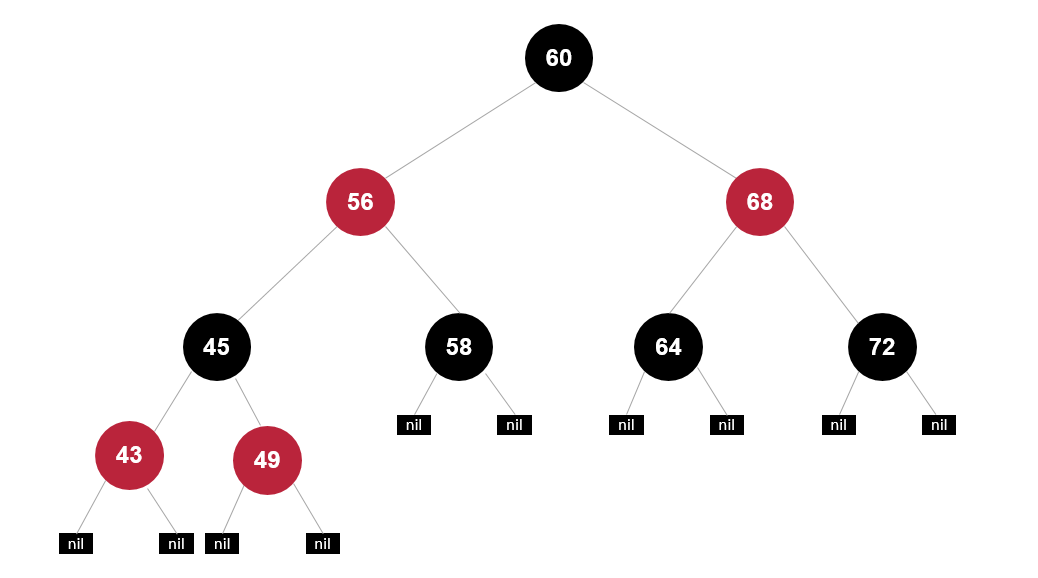
插入51,父节点49,叔叔节点43都是是红色的,破坏了规则4如果一个节点是红的,那么它的俩个儿子都是黑的。需要做出调整
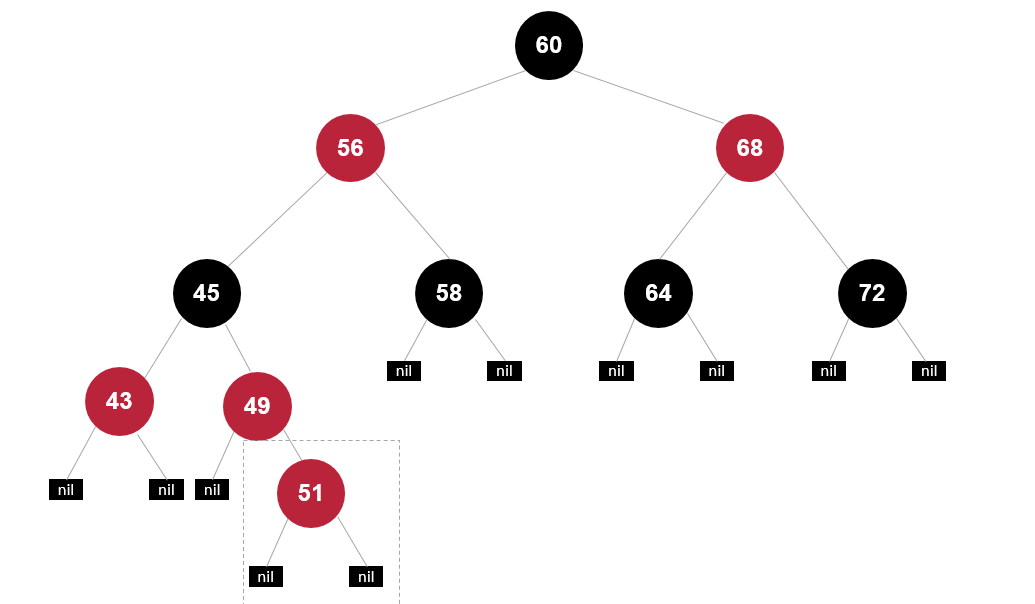
1. 变色
第一次变色后,仍然不符合规则5对于任一节点而言,其到叶节点树尾端NIL指针的每一条路径都包含相同数目的黑节点。
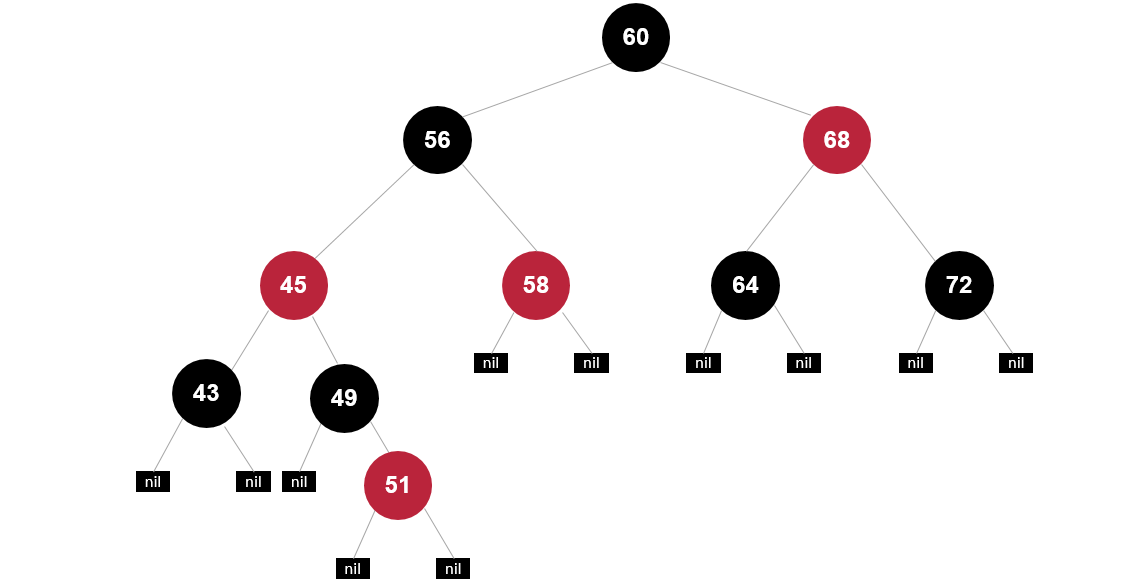
2. 再次变色
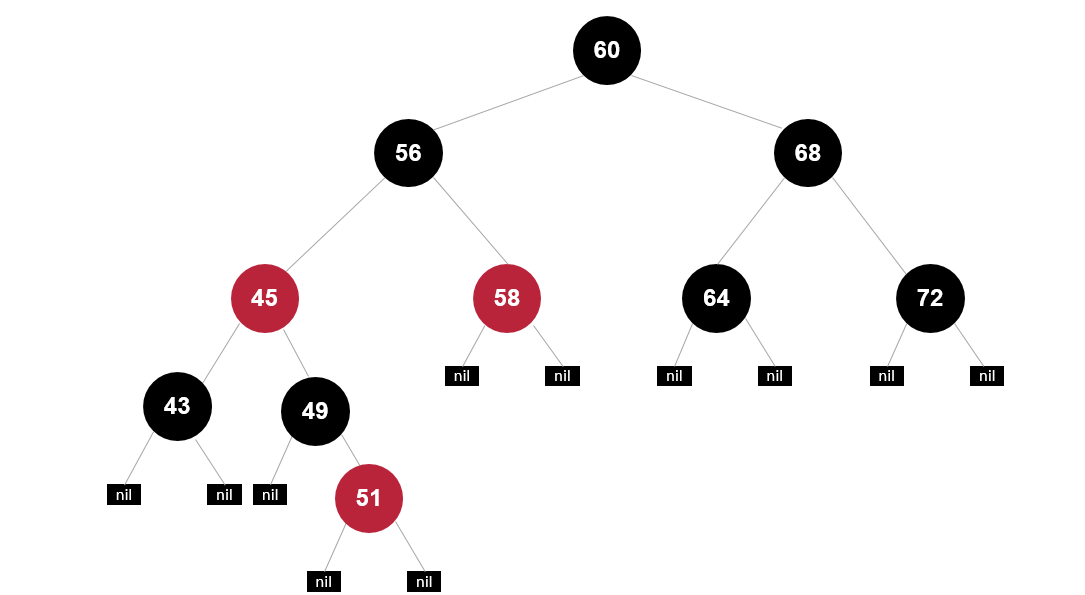
父为红、叔叔为黑(或者null)
左左插入
插入节点40
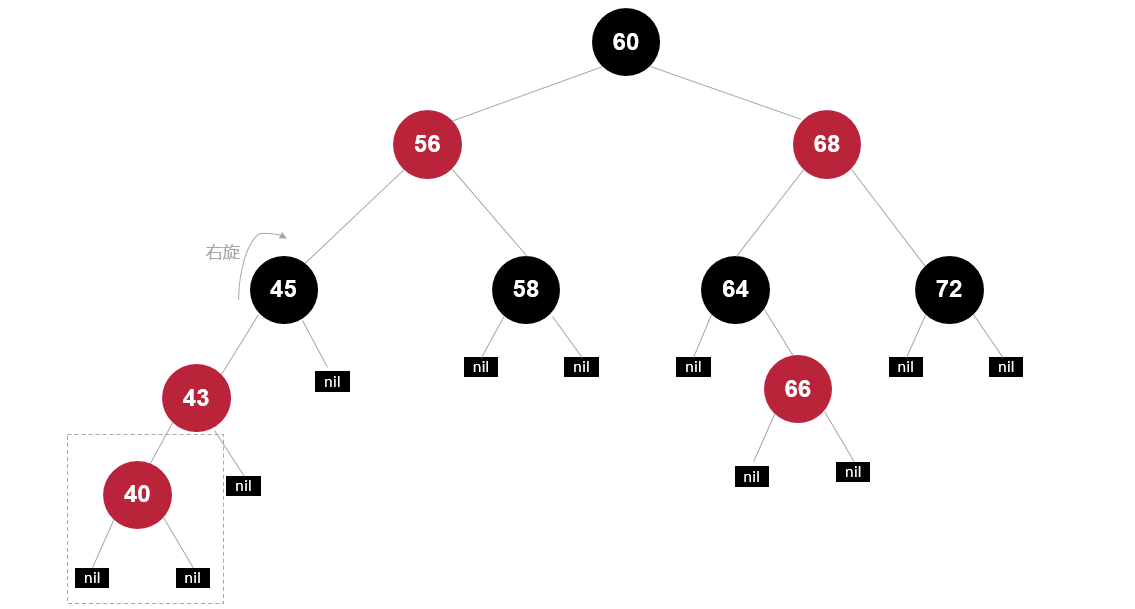
先绕祖父右旋
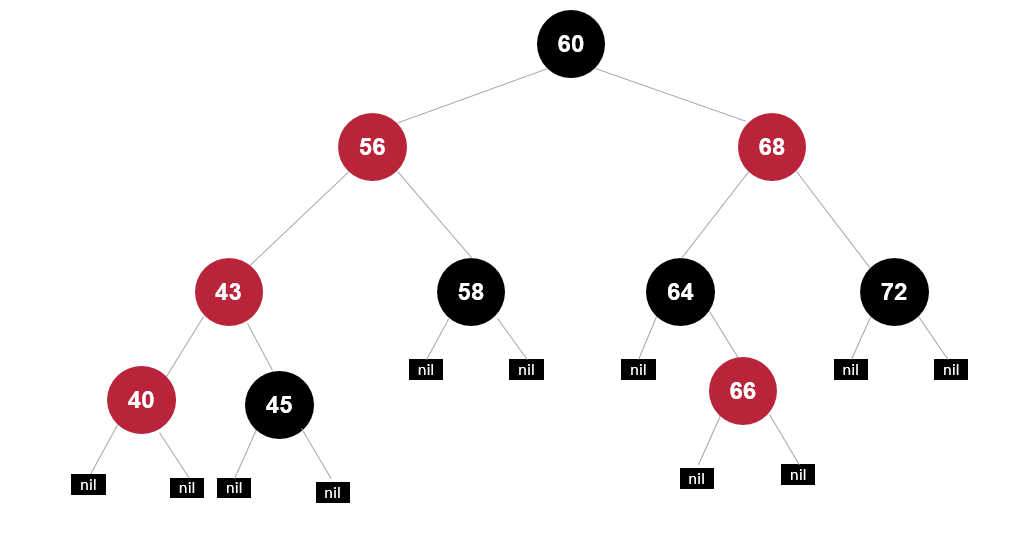
再变色

右右插入
插入节点67
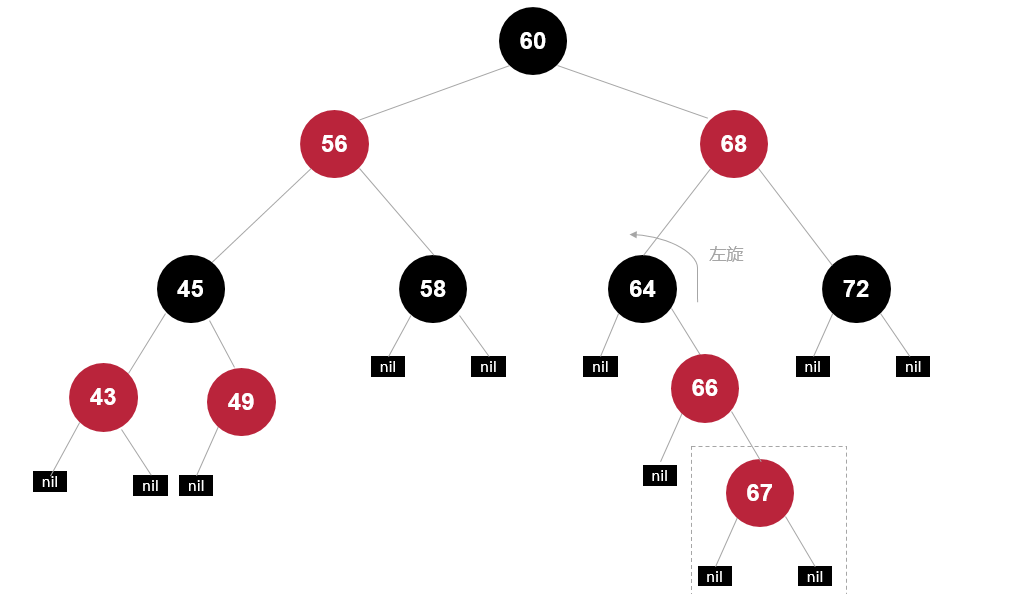
先绕祖父左旋

再变色
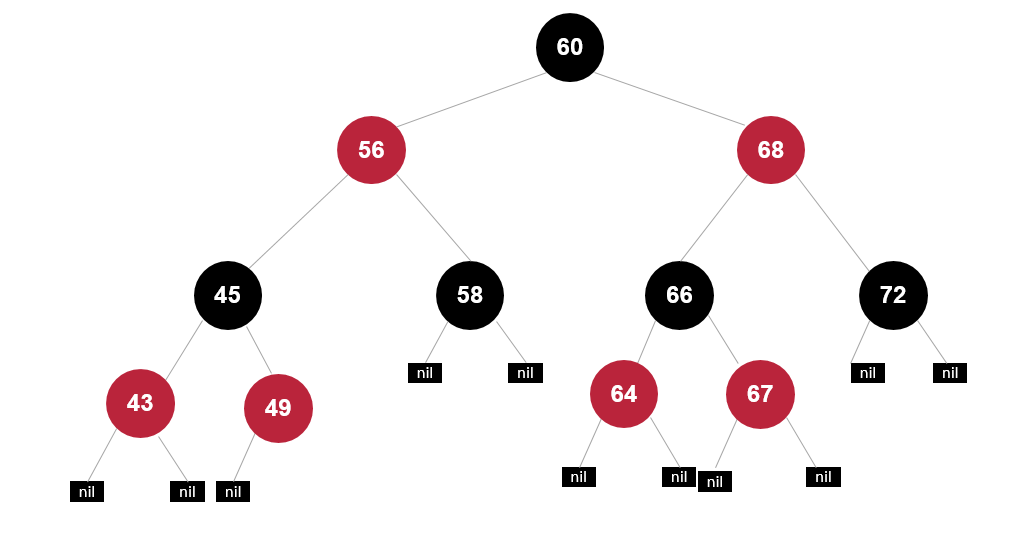
左右插入
插入节点44
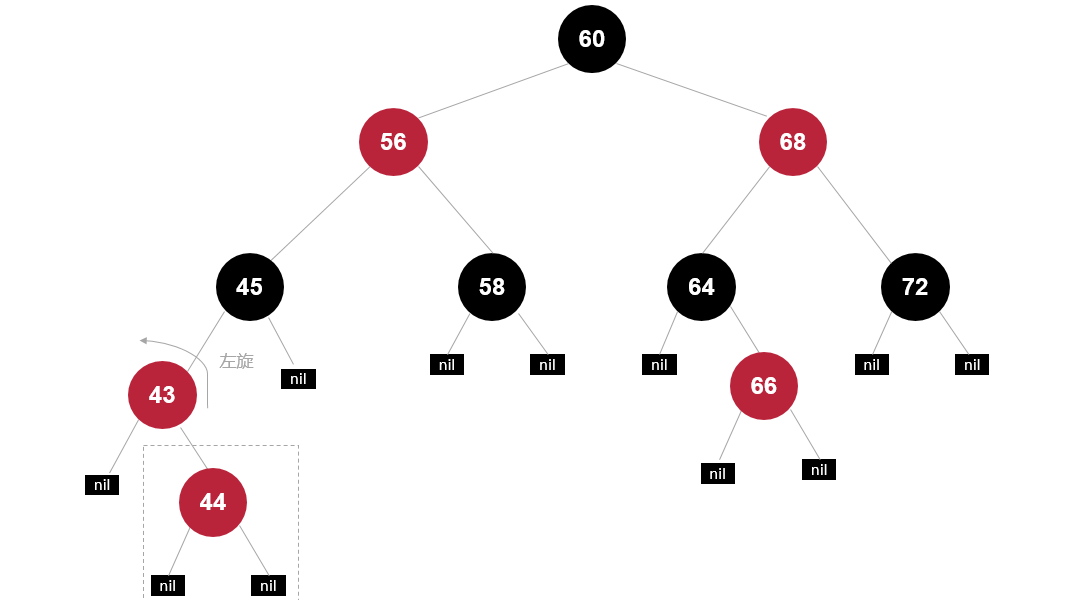
先绕父亲左旋

再绕祖父右旋

再变色
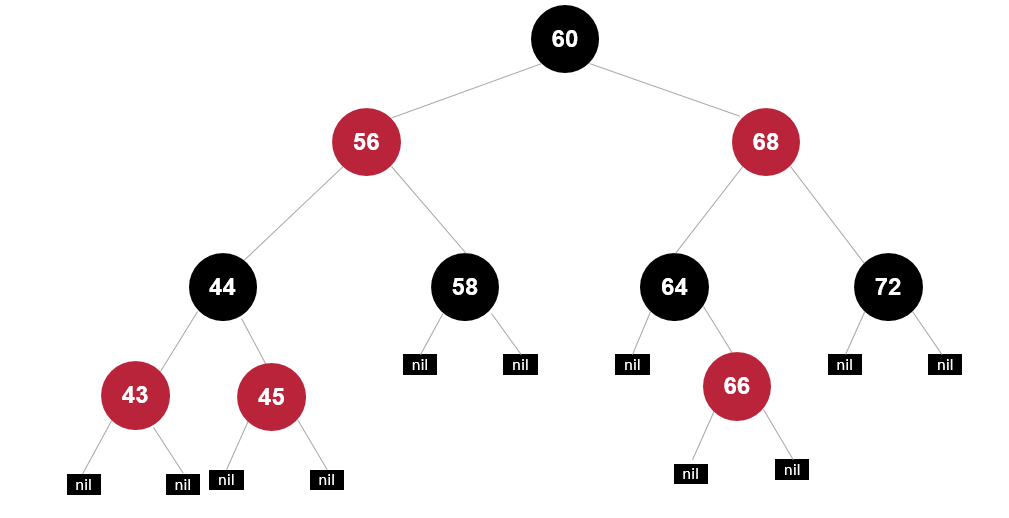
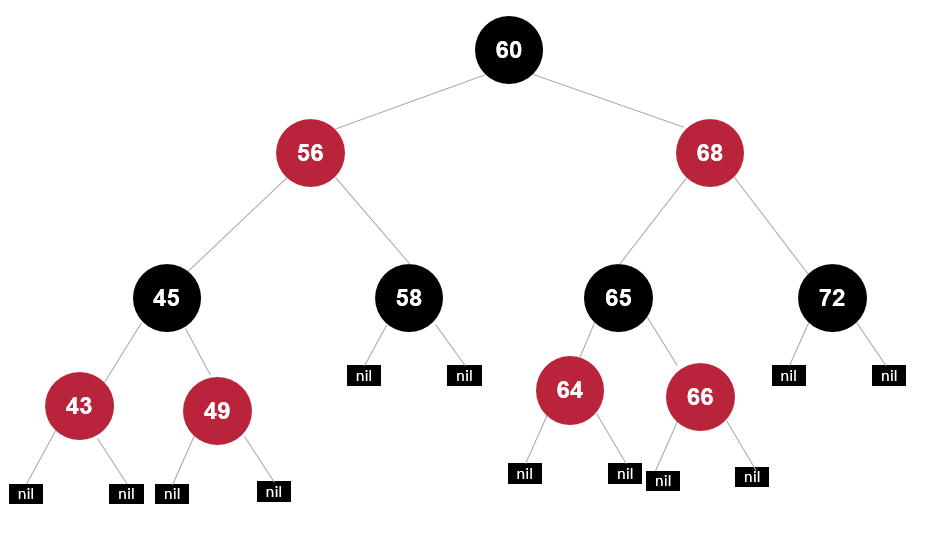
右左插入
插入节点65
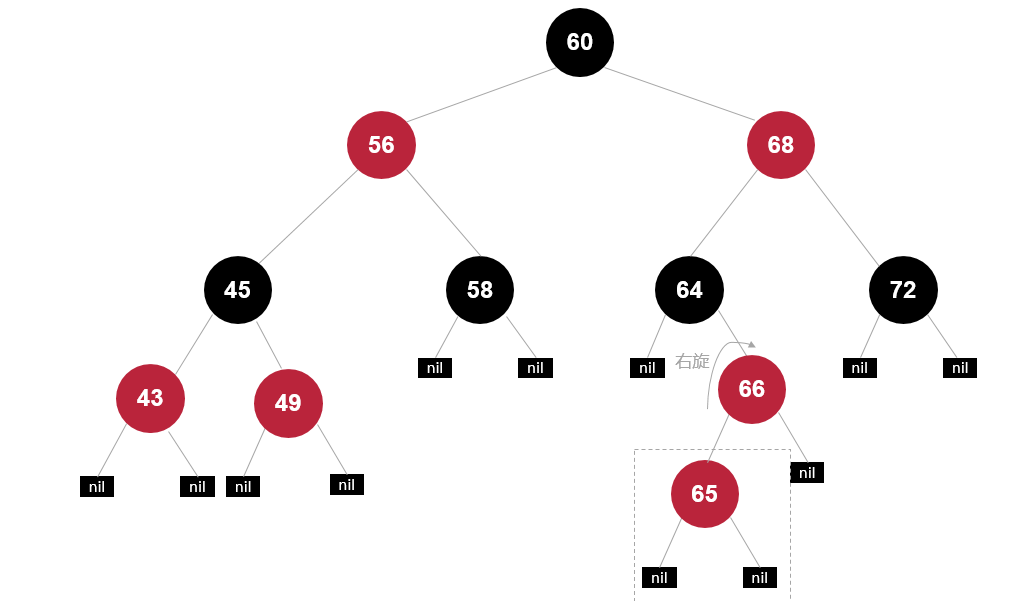
先绕父亲右旋
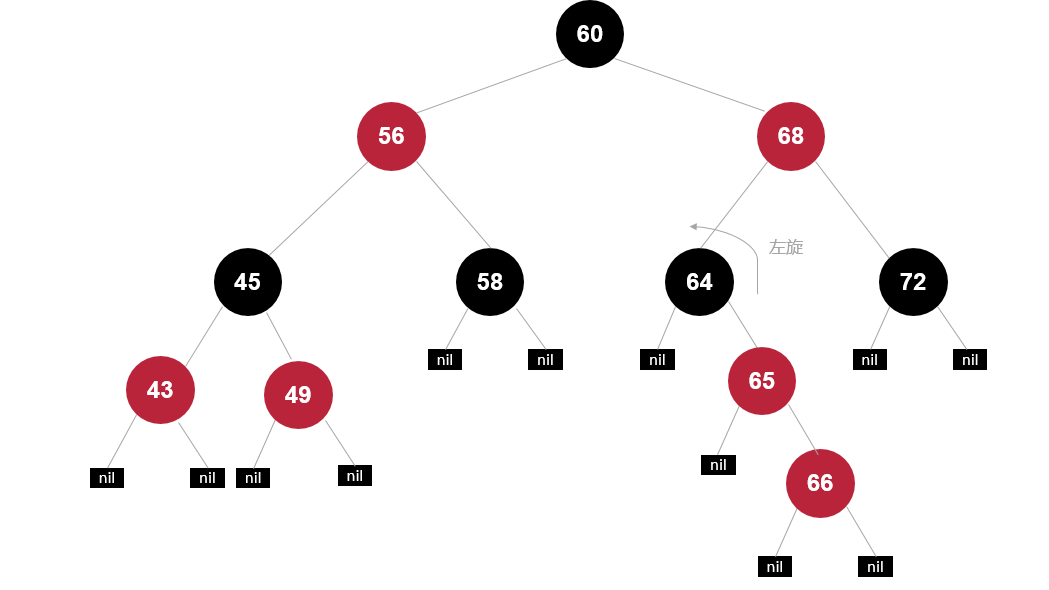
再绕祖父左旋
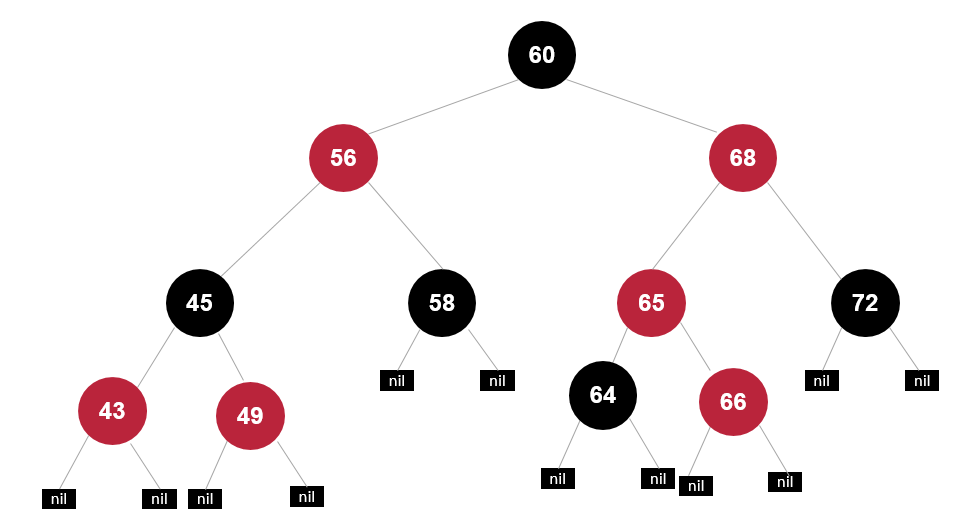
再变色
删除
相较于插入操作,红黑树的删除操作则要更为复杂一些。
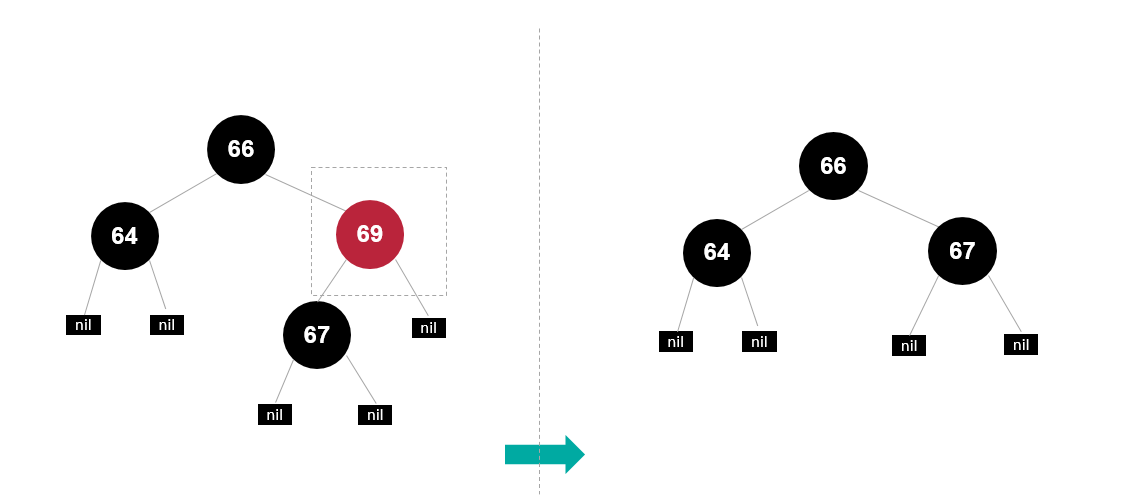
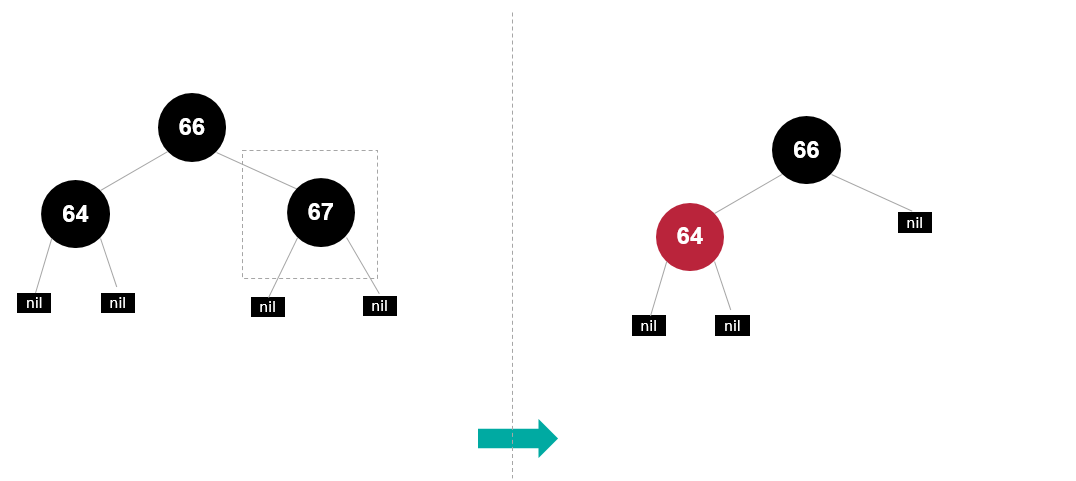
子节点至少有一个为 null
当待删除的节点的子节点至少有一个为 null 节点时,删除了该节点后,将其有值的节点取代当前节点即可。
若都为 null,则将当前节点设置为 null,当然如果违反规则了,则按需调整,如变色以及旋转。
子节点都是非 null 节点
这种情况下,第一步:找到该节点的前驱或者后继。
- 前驱:左子树中值最大的节点(可得出其最多只有一个非 null 子节点,可能都为 null)。
- 后继:右子树中值最小的节点(可得出其最多只有一个非 null 子节点,可能都为 null)。
前驱和后继都是值最接近该节点值的节点,类似于该节点.prev=前驱,该节点.next=后继。
第二步:将前驱或者后继的值复制到该节点中,然后删掉前驱或者后继。
如果删除的是左节点,则将前驱的值复制到该节点中,然后删除前驱;如果删除的是右节点,则将后继的值复制到该节点中,然后删除后继。
这相当于是一种“取巧”的方法,我们删除节点的目的是使该节点的值在红黑树上不存在。
因此专注于该目的,我们并不关注删除节点时是否真是我们想删除的那个节点,同时我们也不需考虑树结构的变化,因为树的结构本身就会因为自动平衡机制而经常进行调整。
前驱为黑色节点,并且有一个非 null 子节点
删除64

找到前驱63,复制后删除前驱

变色

前驱为黑色节点,同时子节点都是 null
删除64
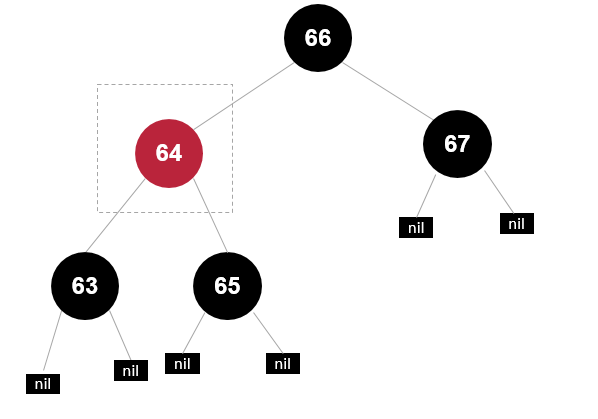
找到前驱63,复制后删除前驱

变色
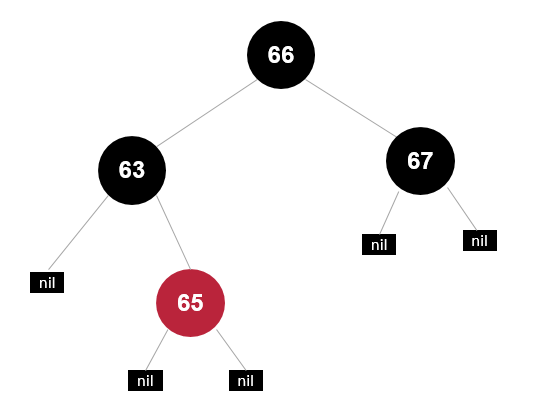
前驱为红色节点,同时子节点都为 null
删除64
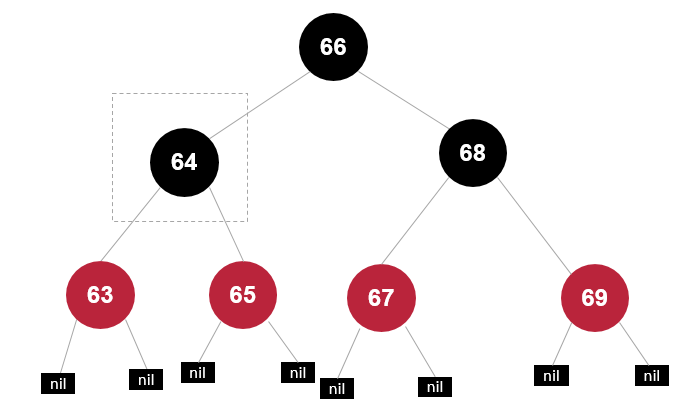
找到前驱63,复制后删除前驱

变色
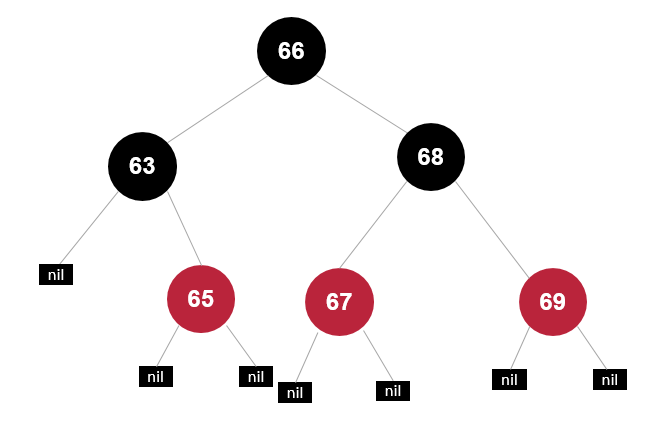
后继与前驱类似
红黑树删除总结
红黑树删除的情况比较多,但也就存在以下情况:
- 删除的是根节点,则直接将根节点置为 null。
- 待删除节点的左右子节点都为 null,删除时将该节点置为 null。
- 待删除节点的左右子节点有一个有值,则用有值的节点替换该节点即可。
- 待删除节点的左右子节点都不为 null,则找前驱或者后继,将前驱或者后继的值复制到该节点中,然后删除前驱或者后继。
- 节点删除后可能会造成红黑树的不平衡,这时我们需通过变色+旋转的方式来调整,使之平衡
java中的TreeMap以及JDK1.8以后的HashMap在当个节点中链表长度大于8时都会用到。
参考资料
https://segmentfault.com/a/1190000012728513
https://cloud.tencent.com/developer/article/1399867
https://blog.csdn.net/qq_34173549/article/details/79636764
https://www.cnblogs.com/ysocean/p/8004211.html
https://developer.51cto.com/art/201908/601688.htm
