基本上都是复制的极客时间的课程
跳表全称为跳跃列表,它允许快速查询,插入和删除一个有序连续元素的数据链表。跳跃列表的平均查找和插入时间复杂度都是O(logn)。快速查询是通过维护一个多层次的链表,且每一层链表中的元素是前一层链表元素的子集。一开始时,算法在最稀疏的层次进行搜索,直至需要查找的元素在该层两个相邻的元素中间。这时,算法将跳转到下一个层次,重复刚才的搜索,直到找到需要查找的元素为止。
- 插入 O(log N)
- 删除 O(log N)
- 查找 O(log N)
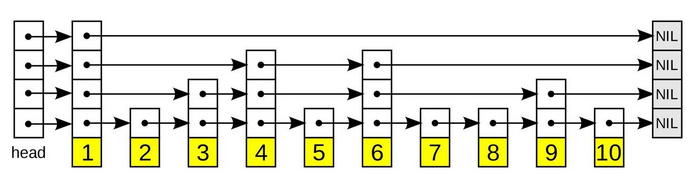
上图是一张跳跃列表的示意图。每个带有箭头的框表示一个指针, 而每行是一个稀疏子序列的链表;底部的编号框(黄色)表示有序的数据序列。查找从顶部最稀疏的子序列向下进行, 直至需要查找的元素在该层两个相邻的元素中间。
对于单链表来说,即使数据是已经排好序的,想要查询其中的一个数据,只能从头开始遍历链表,这样效率很低,时间复杂度很高,是 O(n)。

为了提高效率,我们可以为链表建立一个“索引”,这样查找起来就会更快,如下图所示,我们在原始链表的基础上,每两个结点提取一个结点建立索引,我们把抽取出来的结点叫做索引层或者索引,down 表示指向原始链表结点的指针。
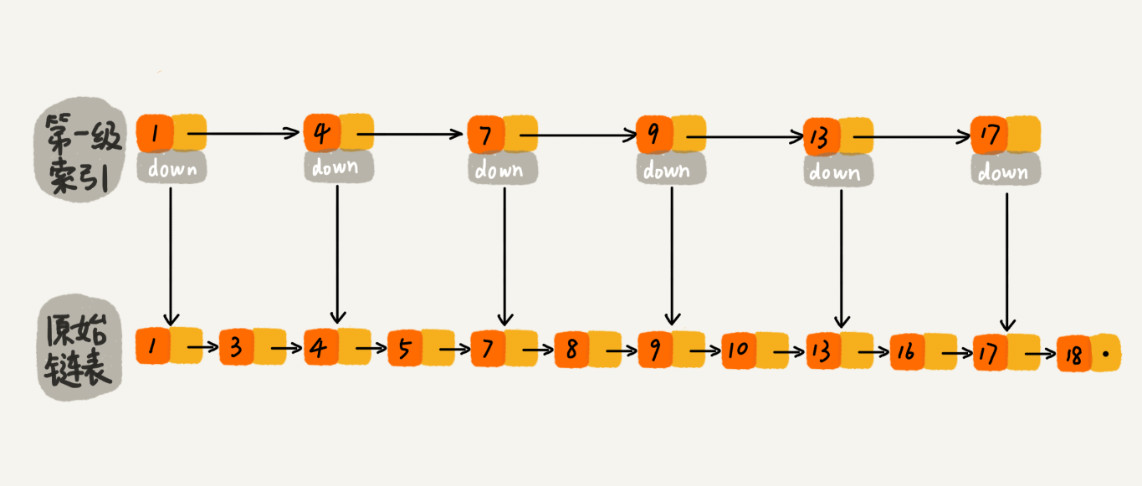
如果我们现在要查找某个结点,比如 16。我们可以先在索引层遍历,当遍历到索引层中值为 13 的结点时,我们发现下一个结点是 17,那要查找的结点 16 肯定就在这两个结点之间。然后我们通过索引层结点的 down 指针,下降到原始链表这一层,继续遍历。这个时候,我们只需要再遍历 2 个结点,就可以找到值等于 16 的这个结点了。这样,原来如果要查找 16,需要遍历 10 个结点,现在只需要遍历 7 个结点。
通过这个例子我们可以看出来,通过建立一个索引层,我们查找一个基点需要遍历的次数变少了,也就是查询的效率提高了。
那么如果我们给索引层再加一层索引呢?
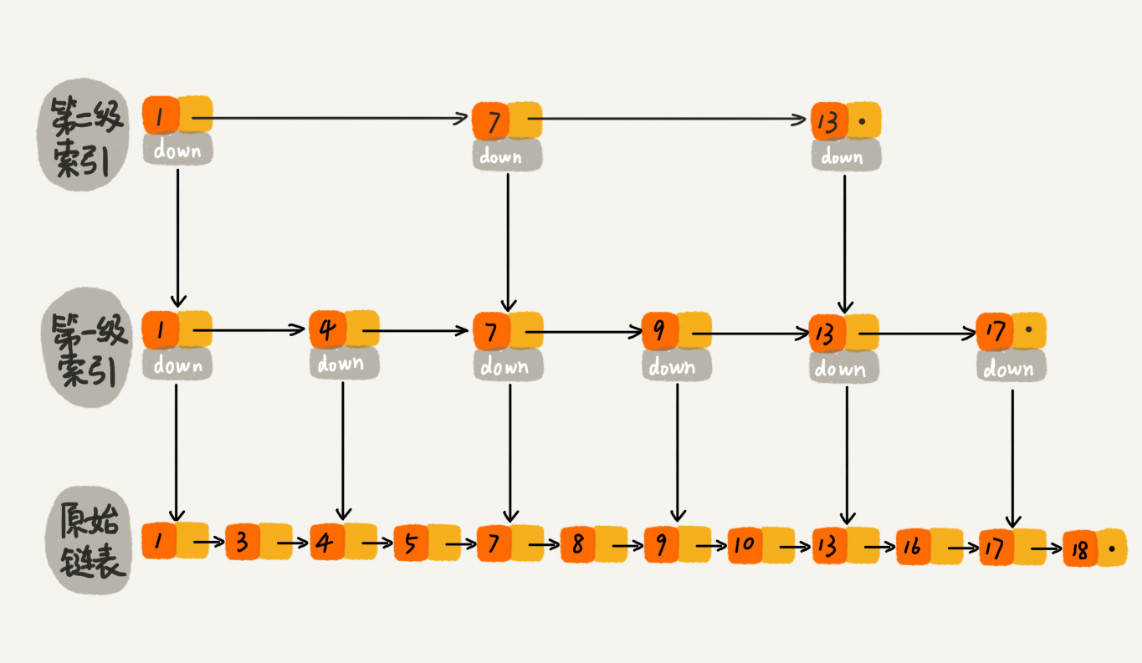
现在我们再来查找 16,我们从第二级索引开始,最后找到 16,一共遍历了 6 个结点,果然效率更高。那么,如果当链表的长度为10000、10000000时,通过构件索引之后,查找的效率就会提升的非常明显。
时间复杂度
先来看这样一个问题,如果链表里有 n 个结点,会有多少级索引呢?
按照我们刚才讲的,每两个结点会抽出一个结点作为上一级索引的结点,那第一级索引的结点个数大约就是 n/2,第二级索引的结点个数大约就是 n/4,第三级索引的结点个数大约就是 n/8,依次类推,也就是说,第 k 级索引的结点个数是第 k-1 级索引的结点个数的 1/2,那第 k级索引结点的个数就是 n/(2k)。
假设索引有 h 级,最高级的索引有 2 个结点。通过上面的公式,我们可以得到 n/(2h)=2,从而求得 h=log2n-1。如果包含原始链表这一层,整个跳表的高度就是 log2n。我们在跳表中查询某个数据的时候,如果每一层都要遍历 m 个结点,那在跳表中查询一个数据的时间复杂度就是 O(m*logn)。
那这个 m 的值是多少呢?按照前面这种索引结构,我们每一级索引都最多只需要遍历 3 个结点,也就是说 m=3。
假设我们要查找的数据是 x,在第 k 级索引中,我们遍历到 y 结点之后,发现 x 大于 y,小于后面的结点 z,所以我们通过 y 的 down 指针,从第 k 级索引下降到第 k-1 级索引。在第 k-1 级索引中,y 和 z 之间只有 3 个结点(包含 y 和 z),所以,我们在 K-1 级索引中最多只需要遍历 3 个结点,依次类推,每一级索引都最多只需要遍历 3 个结点。
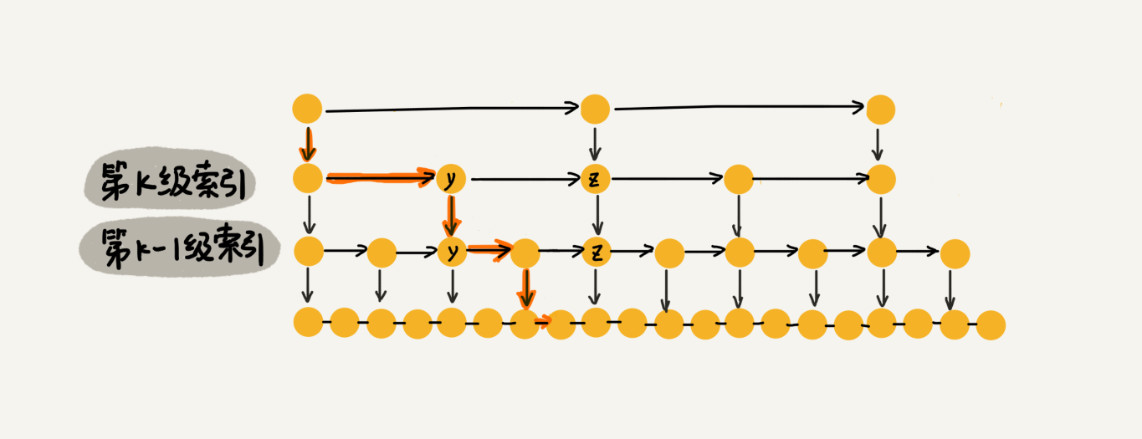
通过上面的分析,我们得到 m=3,所以在跳表中查询任意数据的时间复杂度就是 O(logn)。这个查找的时间复杂度跟二分查找是一样的。换句话说,我们其实是基于单链表实现了二分查找.
空间复杂度
比起单纯的单链表,跳表需要存储多级索引,肯定要消耗更多的存储空间。那到底需要消耗多少额外的存储空间呢?我们来分析一下跳表的空间复杂度。
跳表的空间复杂度分析并不难,我在前面说了,假设原始链表大小为 n,那第一级索引大约有 n/2 个结点,第二级索引大约有 n/4 个结点,以此类推,每上升一级就减少一半,直到剩下 2 个结点。如果我们把每层索引的结点数写出来,就是一个等比数列。
这几级索引的结点总和就是 n/2+n/4+n/8…+8+4+2=n-2。所以,跳表的空间复杂度是 O(n)。也就是说,如果将包含 n 个结点的单链表构造成跳表,我们需要额外再用接近 n 个结点的存储空间。
我们前面都是每两个结点抽一个结点到上级索引,如果我们每三个结点,抽一个结点到上级索引,通过等比数列求和公式,总的索引结点大约就是 n/3+n/9+n/27+…+9+3+1=n/2。尽管空间复杂度还是 O(n),但比上面的每两个结点抽一个结点的索引构建方法,要减少了一半的索引结点存储空间。
实际上,在软件开发中,我们不必太在意索引占用的额外空间。在讲数据结构和算法时,我们习惯性地把要处理的数据看成整数,但是在实际的软件开发中,原始链表中存储的有可能是很大的对象,而索引结点只需要存储关键值和几个指针,并不需要存储对象,所以当对象比索引结点大很多时,那索引占用的额外空间就可以忽略了。
插入和删除
我们知道,在单链表中,一旦定位好要插入的位置,插入结点的时间复杂度是很低的,就是 O(1)。但是,这里为了保证原始链表中数据的有序性,我们需要先找到要插入的位置,这个查找操作就会比较耗时。
但是,对于跳表来说,我们讲过查找某个结点的的时间复杂度是 O(logn),所以这里查找某个数据应该插入的位置,方法也是类似的,时间复杂度也是 O(logn)
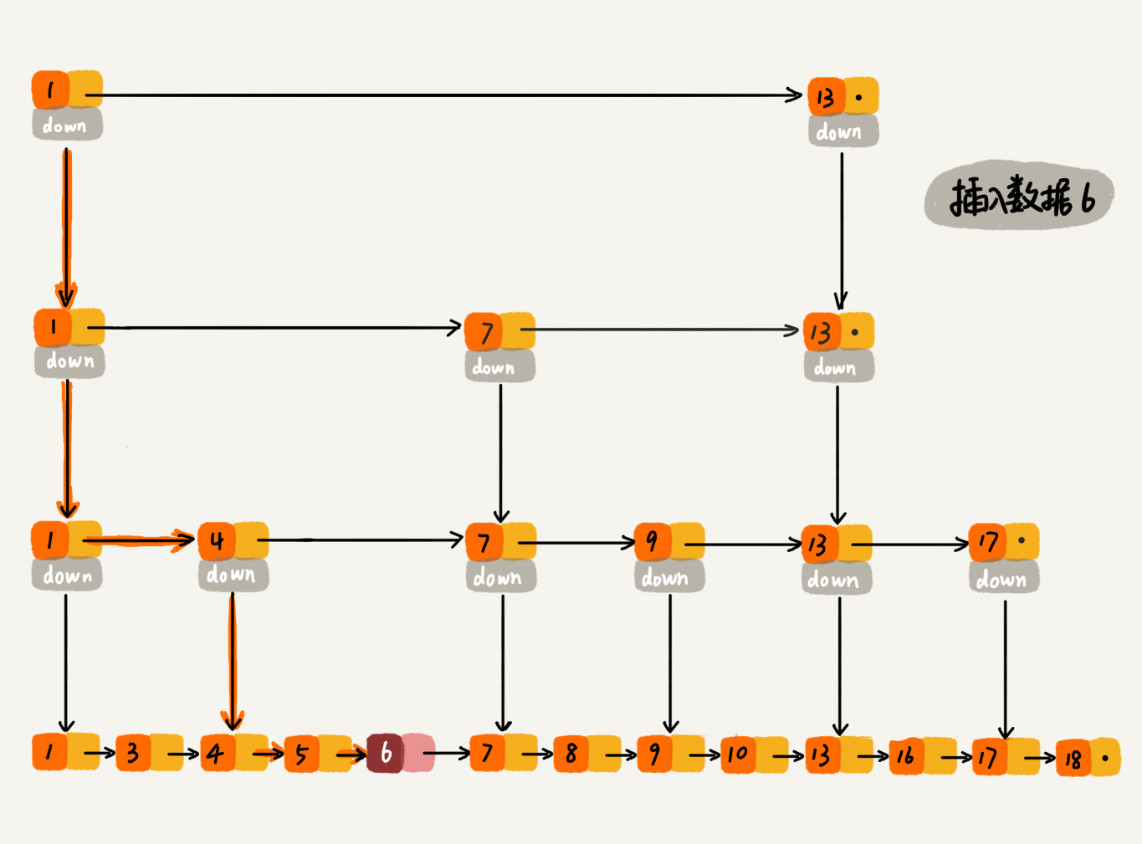
如果这个结点在索引中也有出现,我们除了要删除原始链表中的结点,还要删除索引中的。因为单链表中的删除操作需要拿到要删除结点的前驱结点,然后通过指针操作完成删除。所以在查找要删除的结点的时候,一定要获取前驱结点。当然,如果我们用的是双向链表,就不需要考虑这个问题了。
当我们不停地往跳表中插入数据时,如果我们不更新索引,就有可能出现某 2 个索引结点之间数据非常多的情况。极端情况下,跳表还会退化成单链表。作为一种动态数据结构,我们需要某种手段来维护索引与原始链表大小之间的平衡,也就是说,如果链表中结点多了,索引结点就相应地增加一些,避免复杂度退化,以及查找、插入、删除操作性能下降。
当我们往跳表中插入数据的时候,我们可以选择同时将这个数据插入到部分索引层中。我们通过一个随机函数,来决定将这个结点插入到哪几级索引中,比如随机函数生成了值 K,那我们就将这个结点添加到第一级到第 K 级这 K 级索引中。
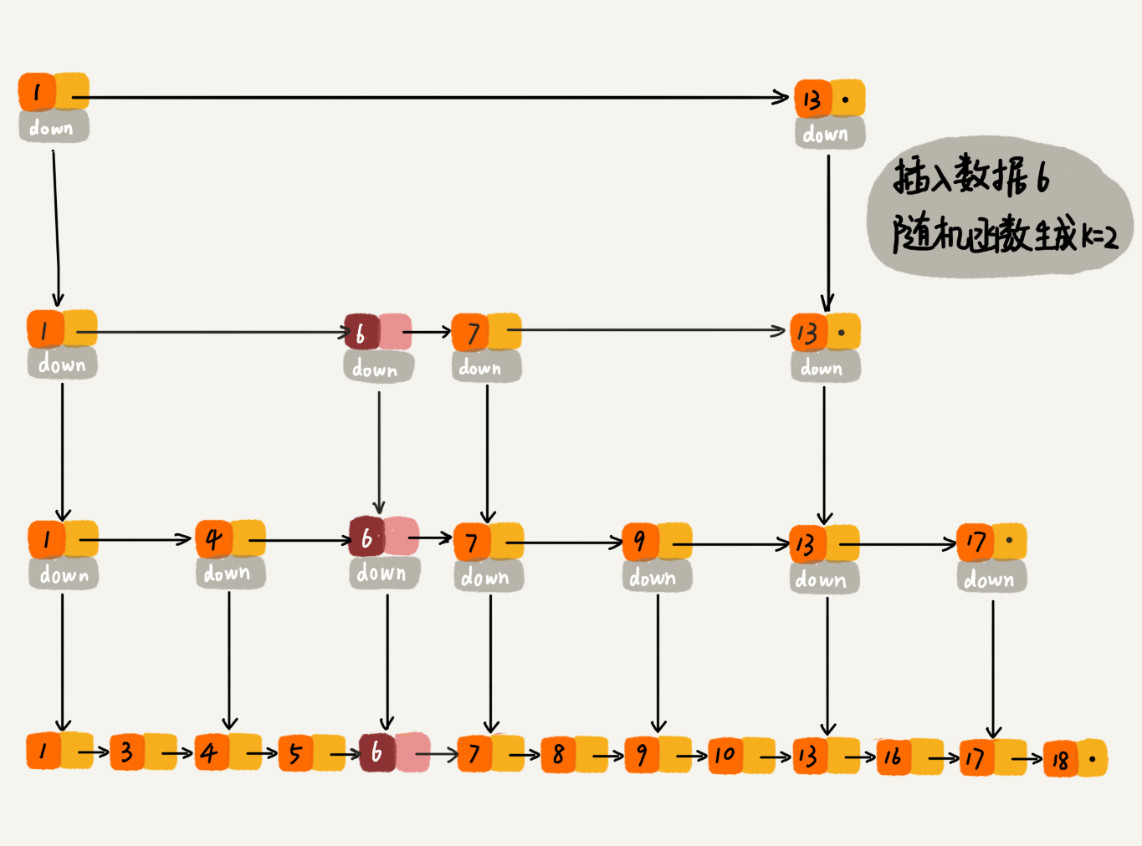
随机函数的选择很有讲究,从概率上来讲,能够保证跳表的索引大小和数据大小平衡性,不至于性能过度退化。
实现
跳表在实现上有两种方式,第一种采用链表实现,第二种采用数组实现,源码太多就不贴了。
链表使用双向链表的实现,每个节点中包含了当前节点的指针,以及向前、向后、向上、向下节点的指针,这种方式比较容易理解。
而采用数组的实现相对来说不容易理解,每个节点都包含了一个节点数组用来表示当前节点的下一个节点,同时这个数组还维持了多个层级的数据,而完成数据的查找。
private class Node<K extends Comparable<K>, V> {
private K key;
private V value;
// 每个节点都包含了一个节点数组用来表示当前节点的下一个节点,同时这个数组还维持了多个层级的数据,而完成数据的查找,比较难理解,debug了好几遍才弄明白
// next[1]表示第一层,next[2]表示第二层
private Node<K, V> next[];
//跨越几层
private int level;
public Node(K key, V value, int level) {
this.key = key;
this.value = value;
this.level = level;
this.next = new Node[level];
}
}
我也是看了别人的源码也无法理解这种实现,最后又搜了一些资料分析了很长一段时间才理解

31-------------------------------------------------------------88-------
14-------18-------21-------31----------------------------------88-------
14-------18-------21-------31-------------------------84-------88-------99-------
14-------18-------21-------31----------------83-------84-------88-------98-------99-------
14-------18-------21-------31-------52-------83-------84-------88-------98-------99-------
对于上面的跳表,总共5层,那么head存储的就是node[5]{14,14,14,14,31},通过node[4].next就得到了将31右侧从第5层遍历到第1层的数据88,88,84,83,52,就得到
同理node[3].next就得到了14从第4层遍历到第1层的数据18,18,18,18,从而node[3].next[2]就得到了14从第4层向右侧遍历到第2层的数据18
如果这时候我们从第4层开始插入一个40,先要从第4层找到每一层距离40最近的节点
while (p.next[i] != null && p.next[i].key.compareTo(key) < 0) {
// 这里就是每层最接近指定key的节点
p = p.next[i];
}
4:31
3:31
2:31
1:31
然后依次将40插入到31的右边
4:head[3].next=40
3:head[2].next=40
2:head[1].next=40
1:head[0].next=40
代码如下:
for (int i = 0; i < level; ++i) {
newNode.next[i] = update[i].next[i];
if (update[i].next[i] != null && update[i].next[i].key.equals(key)) {
oldValue = update[i].next[i].value;
existed = true;
update[i].next[i].value = value;
} else {
update[i].next[i] = newNode;
}
}
理解了新增,对于查询就能理解了:直接遍历每层,找到最接近的节点
Node<K, V> p = head;
for (int i = levelCount - 1; i >= 0; --i) {
while (p.next[i] != null && p.next[i].key.compareTo(key) < 0) {
p = p.next[i];
}
}
if (p.next[0] != null && p.next[0].key.compareTo(key) == 0) {
return p.next[0].value;
} else {
return null;
}
参考资料
http://igoro.com/archive/skip-lists-are-fascinating
https://www.jianshu.com/p/fef9817cc943
https://time.geekbang.org/column/article/42896
https://cloud.tencent.com/developer/article/1422115
https://www.open-open.com/code/view/1453949812917
