堆排序(英语:Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆积的性质:即子节点的键值或索引总是小于(或者大于)它的父节点。
摘自维基百科
堆排序的时间复杂度为 O(nlogn)
堆
了解堆排序之前,我们需要先了解堆,要了解堆首先得了解一下二叉树。在计算机科学中,二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
二叉树在MySQL索引文章中有讲解
堆是一种特殊的树。只要满足这两点,它就是一个堆。
- 堆是一个完全二叉树;
- 堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
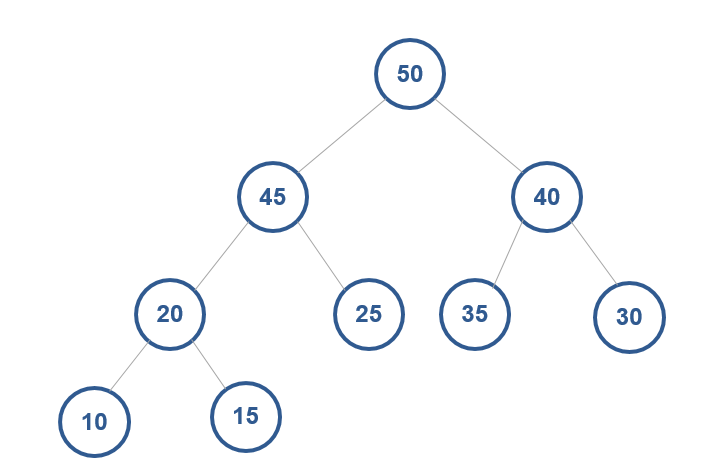
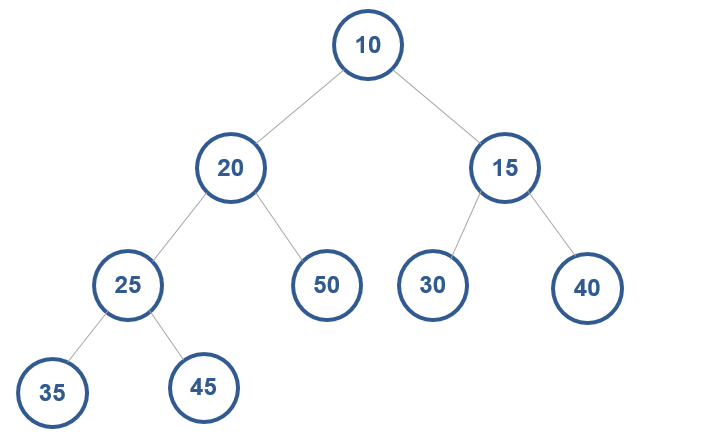
对于每个节点的值都大于等于子树中每个节点值的堆,我们叫作“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆,我们叫作“小顶堆”。
大顶堆
小顶堆
完全二叉树的一个“优秀”的性质是,除了最底层之外,每一层都是满的,这使得完全二叉树可以利用数组来表示(普通的一般的二叉树通常用链表作为基本容器表示),每一个结点对应数组中的一个元素。用数组来存储完全二叉树是非常节省存储空间的。因为我们不需要存储左右子节点的指针,单纯地通过数组的下标,就可以找到一个节点的左右子节点和父节点。
如下图,是一个堆和数组的相互关系
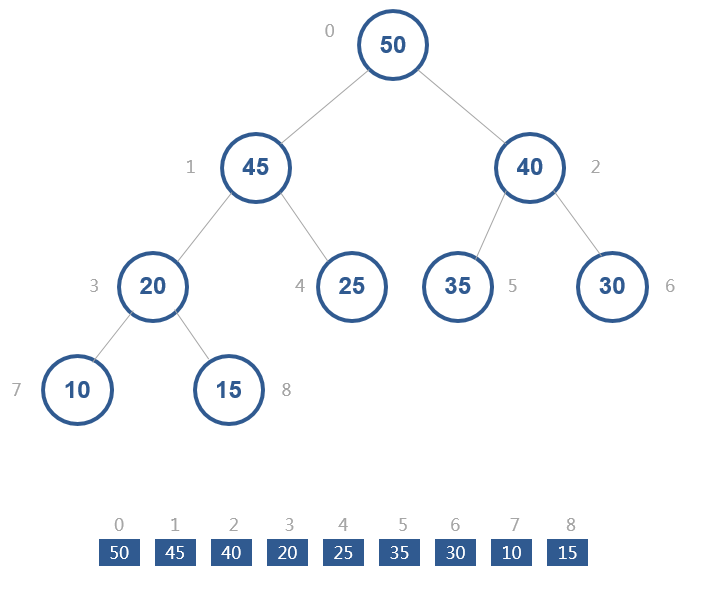
从图中我们可以看到,数组中下标为 i 的节点的左子节点,就是下标为 i∗2+1 的节点,右子节点就是下标为 i∗2+2 的节点,父节点就是下标为 (i–1)/2 的节点。
下面我们以大顶堆为例,讲解对堆的操作
插入一个元素
向下面的堆中插入一个节点48,破坏了堆的特性
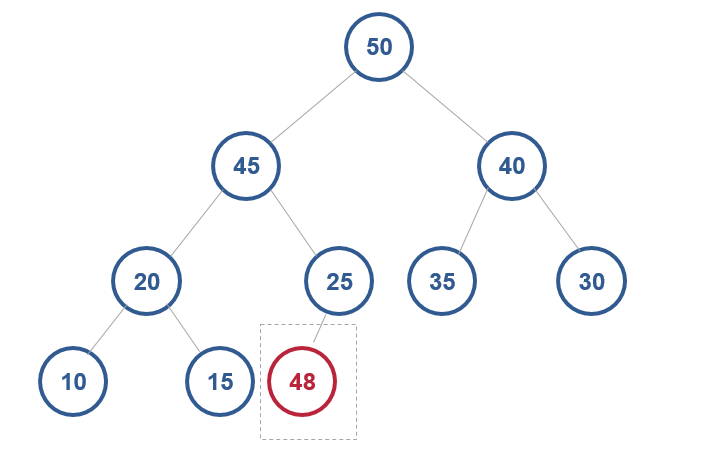
堆化:顺着节点所在的路径,向上或者向下,对比,然后交换。

删除顶部元素
将下面的堆中堆顶节点50删除,破坏了堆的特性。因为堆顶元素就是最大的元素。当我们删除堆顶元素之后,就需要把第二大的元素放到堆顶,那第二大元素肯定会出现在左右子节点中。然后我们再迭代地删除第二大节点,以此类推,直到叶子节点被删除。

完成交换后,发现破坏了完全二叉树的特性
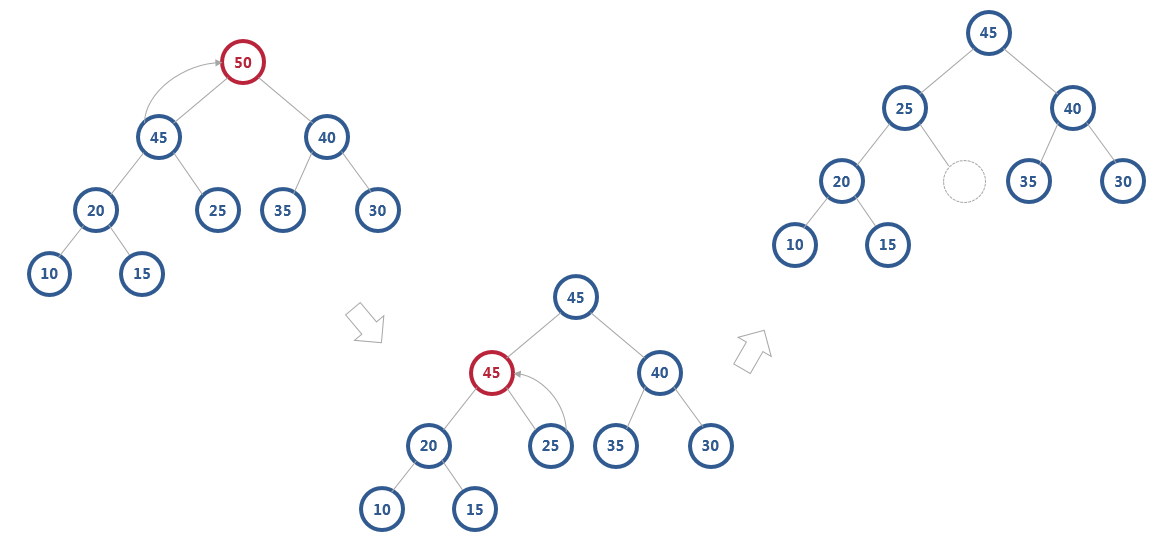
我们需要换一种思路,先用最后一个节点替换堆顶,那么就不会破坏完全二叉树的特性,然后在通过多次交换得到新堆
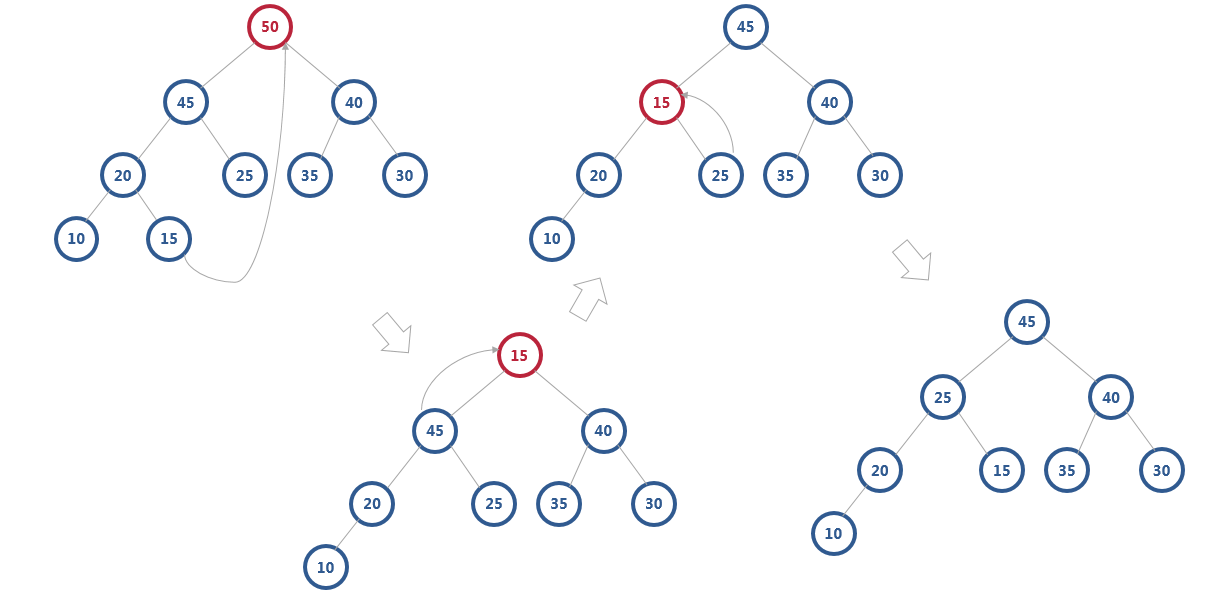
我们知道,一个包含 n 个节点的完全二叉树,树的高度不会超过log2 n。堆化的过程是顺着节点所在路径比较交换的,所以堆化的时间复杂度跟树的高度成正比,也就是 O(logn)。插入数据和删除堆顶元素的主要逻辑就是堆化,所以,往堆中插入一个元素和删除堆顶元素的时间复杂度都是 O(logn)。
堆排序
算法步骤
- 将待排序序列构造成一个大顶堆,此时,整个序列的最大值就是堆顶的根节点。(一般升序采用大顶堆,降序采用小顶堆)
- 将堆顶与末尾元素进行交换,此时末尾就为最大值。
- 然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。
- 如此反复执行,便能得到一个有序序列了
根据上面的步骤,我们可以把堆排序的过程大致分解成两个大的步骤,建堆和排序。
建堆
首先将数组原地建成一个堆。所谓“原地”就是,不借助另一个数组,就在原数组上操作。
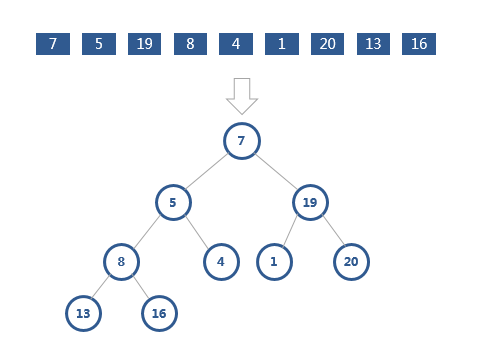
我们选取第一个非叶子节点,从下往上堆化
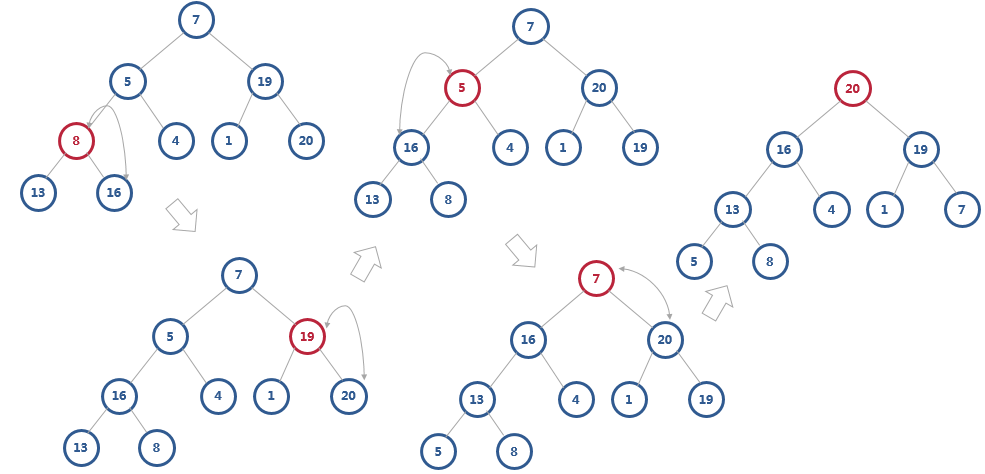
对于完全二叉树来说,下标从
2n+1到 n 的节点都是叶子节点。
建堆的时间复杂度就是 O(n)。
排序
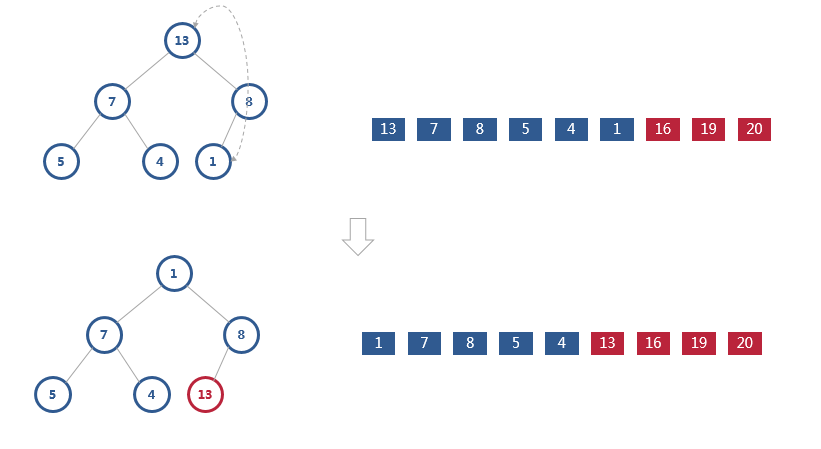
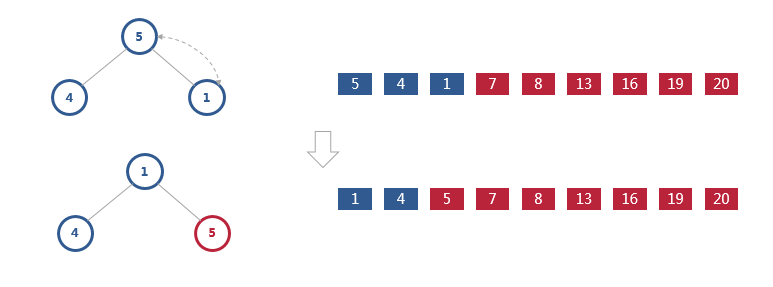
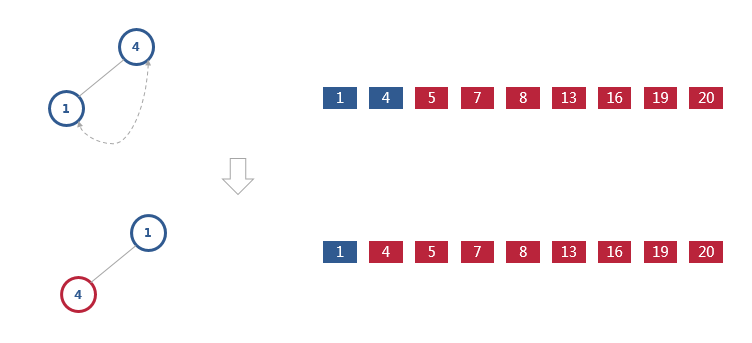
数组中的数据已经是按照大顶堆的特性来组织的。数组中的第一个元素就是堆顶,也就是最大的元素。我们把它跟最后一个元素交换,那最大元素就放到了下标为 n-1 的位置。这个过程有点类似上面讲的“删除堆顶元素”的操作,当堆顶元素移除之后,我们把下标为 n-1 的元素放到堆顶,然后再通过堆化的方法,将剩下的 n−1 个元素重新构建成堆。堆化完成之后,我们再取堆顶的元素,放到下标是 n−2 的位置,一直重复这个过程,直到最后堆中只剩下标为 1 的一个元素,排序工作就完成了。





源码
@Override
public void sort(int[] array) {
buildHeap(array, array.length);
int k = array.length;
while (k > 0) {
SortUtils.swap(array, 0, k - 1);
--k;
heapify(array, 0, k);
}
}
private void buildHeap(int[] array, int len) {
for (int i = (int) Math.floor(len / 2) - 1; i >= 0; i--) {
heapify(array, i, len);
}
}
private void heapify(int[] array, int i, int len) {
while (true) {
int maxPos = i;
int left = 2 * i + 1;
int right = 2 * i + 2;
if (left < len && array[i] < array[left]) {
maxPos = left;
};
if (right < len && array[maxPos] < array[right]) {
maxPos = right;
};
if (maxPos == i) {
break;
};
SortUtils.swap(array, i, maxPos);
i = maxPos;
}
}
参考资料
https://juejin.im/post/5bea6af051882548161b0f02
https://time.geekbang.org/column/article/69913
